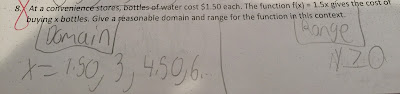Day 52: Graphing

Quote of the Day: “Everything we accomplish happens not just because of our efforts but through the efforts of others.” - Mark Sanborn

Regular Math Objective: Compare and contrast two different linear functions

Regular Math Standards: Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways.

Regular Math Lesson Sequence:

1. Graphing Jumpstart comparing two different graphs. There were some really good conversations that came out of this. Students were able to express that if x was positive  the corresponding y would be negative in one graph, but not the other.
2. QSSQ
3. Review the homework and pepper. The question from the homework we reviewed was the bamboo problem. The text read "bamboo grows at an average of five inches per year." We had a really powerful discussion that was too engaging in one of my classes about what happens as the graph continues to increase over time. We had to look up the fact that bamboo will eventually be capped at 98 feet. We also discussed whether this would be a discrete or continuous graph and if it were truly linear in a real-world sense. 
4. 10 Minutes of the Goldfish lesson from the previous class
5. Exit Ticket that resembled the jumpstart.

It's amazing how the conversations in a class can go from silent to productive by doing two things. Asking kids to share in groups of two to three as opposed to the entire class. I guess it's just a matter of confirming their suspicions, but after giving this time for them to think and hear others thoughts I get much richer responses. The second thing is asking a simpler question of "What do you notice?" It has allowed us to dive into discussions surrounding the words slope, linear, discrete, impossible, real-world, mathematical, quadrants, etc.

Honors Math Objective: Apply the Pythagorean theorem in a real-world context

Honors Math Standards: 8.EE.7, 8.EE.8

Honors Math Lesson Sequence:

1. QSSQ
2. Pepper/HW Review. Right away as students entered I had three students on the marker board writing problems from the homework down. 
3. Dan Meyer's Taco Cart

I've discussed the Taco Cart on a previous post, but I really enjoy this lesson. It went better for this group because fluency isn't as much of an issue and they had two partners that communicated fairly well. 

Day 51: Goldfish Ratio Tables & Graphing

Regular Math Objective: Compare different slopes to determine their real-world meaning

Regular Math Standards: 8.EE.5 Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways. 

Regular Math Lesson Sequence: This is a summary kind of the week because I'm writing it four days into it.

Monday was a disaster with the ants and ladybug problem. It was not scaffolded well. It was also not engaging (scaffolding better could have helped here, but there was still more room for growth).

Tuesday we switched up and went to the Goldfish lesson from YummyMath. We didn't like a few things, so we tweaked the version that YummyMath had put out there.

• The font was weird and distracting. 
• There were too many words that distracted from the math and made it seem more intimidating than it was. 
• Students could easily write the wrong ratios in the wrong table, so we spelled it out for them by putting one ratio into the table. 
• The axes on the graph were not labeled. We labeled one axis to ensure that all graphs would look the same, but still hold them accountable to label the other axis. 
• The third question was too vague. We change give an estimate of 700 to 800 goldfish to 750 goldfish. 
• We neglected to give an example of a ratio table. Probably a mistake. More on that below. 

Here was our goldfish activity. 

The first day of the lesson the students spent the entire time on question one putting together the ratio tables. It was like pulling an anchored boat to shore. On Day Two, we eventually got to answering the second and third questions. Even this was an adventure. By Day Three, we finally were able to graph and discuss the steepness. Most students could not answer the seventh question because of time constraints. 

The lesson was worth it, but I would tweak this further. In the future, I would eliminate the fourth question. I would also provide all of the information for the first two ratio tables to cut the time spent on that aspect of the lesson down. I would spend significant time reteaching the vocabulary of ratios, unit rate, and proportion. I also would alter the format on the last question. The students are asked to do four different things within the framework of this one question, so I would isolate each of those three things to make it explicit what they are being asked. 

Honors Math Objective: Apply the Pythagorean Theorem to find the distance between two points in a coordinate system. 

Honors Math Standards: Apply the Pythagorean Theorem to find the distance between two points in a coordinate system. 

Honors Math Lesson Sequence:

1. My Favorite No. I explained nothing. Students all got either four or two units for the distance between the points (-2,-1) and (0, 1). I then did not even go over it with them. They were so angry. 
2. QSSQ
3. Exploration. Students discovered that two points distance can be discovered by just using the Pythagorean theorem with a third point. 
4. The exit ticket was My Favorite No. It was amazing to see that virtually the entire class went from not being able to do a problem to all of them being able to do a problem with just a tiny bit of prompting from me. 

Day 50: Ant and Ladybug Disaster

Quote of the Day: “It can be seen that mental health is based on a certain degree of tension, the tension between what one has already achieved and what one still ought to accomplish, or the gap between what one is and what one should become.” - Victor Frankl

Regular Math Objective: Differentiate between two lines in a graph

Regular Math Standards: 8.EE.5 Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways.

Regular Math Lesson Sequence: This was the resource that was used for the entire agenda.

1. Students discussed what they noticed and wondered when looking at two graphs. It was easily the best part of the lesson. 
2. I had the students first count where the ladybug and the ant were on the number line. The attention to detail was extremely important. If you look closely at the number line, the head of the insects is where to count. I for one was caught off guard. This is excellent for getting students to stop and think. It's a higher level concept inside a higher level concept. We weren't ready for it though. The directions say "constant rate of change." I really had to spell that out for students. 
3. After we looked at each insects distance after a certain amount of time, I had students discuss the ratios. They were not able to articulate what a ratio was. That made it really hard for us to talk about proportions. If I were to do it over again, this is where to begin. It's not as if students do not get ratios and proportions in prior grades. As a former sixth grade teacher for many of my current students, I can personally attest that we talked about ratios at least twice per week. If it doesn't matter to kids though eventually they will forget. And that happens to be the case here. Not for all of them, but for a critical mass of them that forces my hand to pump the brakes. 
4. We answered the four questions about multiple representations. Students had a difficult time placing the graph with the correct bug. There were definitely students that were successful and that learned. It just felt very painful and students didn't show any joy, curiosity or any other positive emotion. It could have been the long weekend, but I also think the background knowledge was not strong enough to do this lesson at this point.

Honors Math Objective: Derive the Pythagorean theorem

Honors Math Standards: 8.G.6 6. a. Understand the relationship among the sides of a right triangle. b. Analyze and justify the Pythagorean Theorem and its converse using pictures, diagrams, narratives, or models.

Honors Math Lesson Sequence:

1. Pass out self-assessment sheets
2. Review the functions quiz as a whole group
3. Students were given a picture of two different pictures and told to determine why a-squared plus b-squared equals c-squared. The cat was already out of the bag on the formula, so asking that to get the formula would be too easy. Asking them to determine why the formula is what it is was more fun.
4. I had students write for 90 seconds everything they knew from the drawing. I then had them share out what they wrote in groups of three. Finally they shared out to the larger audience. From there we were able to break down the problem with my help. 
5. Kinesthetic learning of what the hypotenuse, legs, and right angle were to the right triangle. 
6. Assign the homework.

Day 49: Finding the Domain and Range Errors

Quote of the Day: “Two young women told us that they have just returned from Iraq after having their HET truck disabled when an insurgent’s bullet went through the engine block. ‘It was a lucky shot,’ one of them said. Even if the insurgent had been aiming there, it would be highly unlikely to get that result.’ When asked what they did when the truck was disabled they said ‘We were taking fire and just hunkered down, protected the vehicle, and waited for reinforcements to arrive. We’re not just going to leave it there.’ As we parted, they thanked us for being there. I told them we should be profusely thanking them, and we did. Then one of them said, ‘you don’t have to be here. We do.’I could not believe how committed and courageous those two soldiers were. In our time at Camp Arifjan we found that was the rule rather than the exception.” - Jay Bilas

Question of the Day: "When we substitute for f(x) should we keep the (x)?" "How do we know to divide when Dan is on the sand for 2 feet per second instead of multiply by 325.6 feet?"

Regular Math Objective: Get better

Regular Math Standards: 8EE1 - 8EE4, NS.1, NS.2, 8.G.6 - 8.G.8

Regular Math Lesson Sequence: Catch Up Day

My overall take from this day was that it was good to give students the opportunity to improve and even better that some students took advantage of the opportunity. Timing this day right before a long weekend is advantageous because it did not make sense to start an entirely new unit and we are also one week from marks closing.

That said, some students did not get better. That's not to say that they made classroom management hard on me, but I had a few students just do TenMarks assignments and because I was busy with correcting other students quiz retakes and giving them feedback, I never got to provide feedback or prompting for students on TenMarks. It was not until evaluating their work afterward that I saw that some of the students who "were on TenMarks" did not submit anything from TenMarks. These also happened to be the students that needed to have a catch up day the most because they have failed assessments. I could have done a better job regulating what students should and should not be doing especially because the students that struggle the most struggle partially because they lack goal-directed behaviors.

One mistake worth noting from today. Many students it seemed made this subtraction error:

Honors Math Objective: Identify if ordered pairs, input out tables, and graphs are functions; use function notation to solve problems in a mathematical and real-world context; give the domain and range of discrete and continuous functions

Honors Math Standards: A1.F-IF

1. Understand that a function from one set (called the domain) to another set (called the range) assigns to 
   each element of the domain exactly one element of the range. If f is a function and x is an element of its domain, then f(x) denotes the output (range) of f corresponding to the input x. The graph of f is the graph of the equation y = f(x). 
2. Use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context. 

Honors Math Lesson Sequence: Students took the quiz. There were huge issues surrounding how they found the range. Unsurprisingly, the main reason they struggled was because the teacher (that's me) misled them. On the study guide, I made two crucial errors that I will admit to them (after they put their tomatoes in their lockers). The range for both questions 6 and 8 were corrected by a student in red ink here. As it turns out, number six the range should have been less than or equal to 8. In the second one, I said the range was greater than or equal to 7, but that would be the case if the domain was greater than or equal to 1 (which it wasn't).

When they say I should pull their grades up because I messed up I will say that I deserve a retake. That's how I handle their mistakes so it's good to be a classroom that allows retakes for literally everything on virtually any day. If I were to make an honest prediction, I actually think the kids will not complain that I made an error. They're pretty forgiving, but we'll see. Here were the mistakes of the students from the quiz:

I have no theory for why the student believes it has to be all even integers. And also why the range would then be just four specific points given such a large domain. Thus, it would be a great question to pose to the entire class when we go over it.

Why can't x be zero? And how can x be 0.5?

Water here! Get your ice cold water here! 

-Waterboy, I'll take one. 

Sorry sir we don't provide the option of buying one. You can buy 1.50 bottles if you like. That way if you are still thirsty after one, but won't finish two you'll have your thirst properly satisfied without the guilt of wasting a precious resource!

Ok so I can make fun of these I suppose, but I'll also be ready for the abuse to come right back on me since I'm the one that started all of this getting the domain and range wrong stuff anyway. 

Day 48: Dan Meyer's Taco Cart

Regular Math Objective: Apply the Pythagorean theorem in a real-world context

Regular Math Standards: 8.G. 6a. Understand the relationship among the sides of a right triangle. b. Analyze and justify the Pythagorean Theorem and its converse using pictures, diagrams, narratives, or models.

8.EE.7 Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.

Regular Math Lesson Sequence: Today's (Wednesday) lesson came off the heals of a professional development we had in the district all day Tuesday so the kids had the day off. We had to pick up from where we left off on Monday, which unfortunately was an awkward place. These five things had happened Monday.

1. I had shown the classes Act I of Dan Meyer's Taco Cart. 
2. In partners, students provided the question that we needed to consider. Who will arrive to the taco cart first - Ben or Dan? 
3. They made a prediction to who was going to be first to the Taco Cart.
4. I asked them and their partner to determine what information would be needed and they gave me the bits that made solving the problem a possibility. 
5. I revealed the information about the speed on sand versus the speed on land as well as the distance of the legs of the triangle courtesy of the link above. 

Almost 48 hours later I knew that to ask students to recall one of those five things let alone all of them was a tall order. So we did a quick recall of all five things which helped get the absent kids up to speed and also set the stage for the rest of the class. From that point, I spent the entire lesson getting the students to answer four questions. 

What is the distance Dan will walk? 

I thought for sure this was a gimme, but it wasn't. What was very revealing was that students who drew a diagram did much better than those who did not. Some students subtracted for some reason that I do not know. The most common error though was that they wrote down the Pythagorean Formula. That's what their instinct is. And to be honest I cannot blame them or even scold them. If they get just one picture of a triangle on a standardized test this year, I would put my mortgage on Señor Pythagoras being called upon. This is exactly why I made this a question within the context of this lesson though. I wanted to see students think about this. Per usual I made every effort not to tell students what to do. Unlike other days though where I hurriedly send them in the right direction, today I was determined to take my time with just these four questions so the students were able to uncover their own misconception. Onto Question 2:

How much time will Dan take to get to the taco cart? You can use a calculator if you want but show what numbers are being calculated. 

At the professional development yesterday we spent about an hour discussing writing in math, which morphed into students explaining their work in some way. Everyone in the room was familiar with the same reactions.

T: What do you think you'll do? 

S: Multiply. Teacher gives confused look. Divide. Add? 

And with this "guess to get by" line of answering in mind, I was asking students that answered this question about Dan's time incorrectly and correctly the same questions. Why did you do that? About literally every number and operation in the problem. Some students were dividing the total distance that Dan walked by five. They were ignoring that he is slower on the sand. Some students had the correct steps on their paper, but they got that information from their partner and had not bothered to inquire why the numbers were the way that they were. Some students had actually done out the correct steps on their own, but had a much harder time articulating it. Other students were just plain old stuck. For these students I reminded them of George Polya's problem solving strategies. We broke down what was already known and what we were trying to find. Then we discussed strategies. We ha already drawn a picture. Had we tried a chart? Had we tried a similar number? And next thing you know we were trying both as students were determining how much time moving two feet, four feet, and six feet would take in the sand. From there we could attack the more intimidating numbers. 

My favorite part though was the unintended consequence of the math in this problem that seemed to happen once per class today. Students were successful in everything they did until it came to converting seconds to minutes.

Again, we made a chart. We looked at how 240 seconds was 4 minutes and 300 seconds was 5 minutes. How was 275 seconds so close to 5 minutes? We also discussed what 4.5 minutes was a fraction. And finally I had to show them a proportion for a cherry on top of what the error was. Deep Breath. Question 3:

What was the distance that Ben traveled?

They did really well with this. Again they were dying to use a-squared plus b-squared equals c-squared from the moment they saw the right triangle. It's like running into Johnny Drama from Entrourage in real-life and restraining yourself from yelling 'Victory!' True story that really happened to me, but I didn't restrain myself. 

The beautiful unintended consequence was that they had no clue where to find the square root button on some of the calculators. Standard for Math Practice 5 - learning to use appropriate tools strategically. Check. On to Question 7:

How much time will it take Ben to arrive at the taco cart? 

By this time, they were ready for this question. It was easier than the question they had done with Dan's time because Ben was on the sand the whole time. The issue for many students though was that the difficulty of Dan's time had caused them to avoid this. At this point in the lesson going from each partnership and really digging deep on the questions I asked was taking it's toll on classroom management. I kind of let things go today. I did not want to stop the class for risk of revealing information that they discovered. The lesson itself was extremely engaging and some kids took off and ran. The ones that did not would have struggled regardless of what I did, so for today I just kind of let them drift a little until I had the chance to intervene. 

Overall this lesson was well worth the time - even though I had already quizzed the students. Many of them were excited to be able to solve a real-world problem with something as complicated as what we had done with a fancy formula. 

Honors Math Objective: Identify if ordered pairs, input out tables, and graphs are functions; use function notation to solve problems in a mathematical and real-world context; give the domain and range of discrete and continuous functions

Honors Math Standards: A1.F-IF

1. Understand that a function from one set (called the domain) to another set (called the range) assigns to
   each element of the domain exactly one element of the range. If f is a function and x is an element of its domain, then f(x) denotes the output (range) of f corresponding to the input x. The graph of f is the graph of the equation y = f(x).
   
2. Use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context. 

Honors Math Lesson Sequence: The entire lesson was the study guide. Students had the biggest issue with defining the range for a problem in which an equation and the domain were given.

Quote of the Day: “Which relationship is most strained in your life right now? What would it look like if you began focusing on that person’s best moments and sought to affirm them?” – Dale Carnegie

Day 47: Pepper with Function Notation

Quote of the Day: “Talking about what went wrong rather than who went wrong will make those around you much less defensive.” - Mark Sanborn

Question of the Day: "Does spelling count?" This was a reference to the word hypotenuse on the quiz. "Doesn't f(x) mean multiply?"

Regular Math Objective: Correct past errors regarding Pythagorean Theorem and scientific notation

Regular Math Standards: 8.G. 6a. Understand the relationship among the sides of a right triangle. b. Analyze and justify the Pythagorean Theorem and its converse using pictures, diagrams, narratives, or models.
8.EE.7 Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
8.EE.8 Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.

Regular Math Lesson Sequence:

1. I had students fill out their self-assessment sheet. The first question that was asked was did you do the study guide at home and why or why not. The second question that was asked was how would you feel about a potential catch up day and would you be willing to help classmates at such a day. I did not read responses to the first question yet, but the response to the second question was in favor of catch up day. My honors class has already successfully implemented catch up day, so I talked to the class about how important peer teaching was to the entire process. 
2. Students worked in partners to correct at least one of their mistakes on a marker board. This is either the second or third time I've used this routine following a quiz this year with these particular students and I am finding that some of them are getting worse at it rather than getting better. In order to get students to work I have to say individually to them to write down their mistake either on the marker board or on the quiz. 
3. We did a think aloud regarding catch up day. 
4. I started Act 1 of Dan Meyer's video of the Taco Cart and passed out this sheet. Students then conversed amongst one another about what potential math questions came out of this answer. We debriefed as students all came to a consensus around the general theme of who will be first to the taco cart? 
5. They made predictions about who would be first. It was nice to hear them use math vocabulary as they referred to the paths because they were actually talking to each other rather than to me. In other words, they were not afraid to sound like a nerd. 
6. We discussed what other information would be relevant to solving this problem, and I showed them the information that they would need in order to solve. 
7. Time ran out and we went our ways. Next class we will revisit Pythagorean Theorem as it is a short week, so I'm actually going to sneak in a catch up day on Thursday before Veteran's Day. 

Honors Math Objective: Identify the coordinates given a statement of function notation; apply and analyze function notation in a real-world context

Honors Math Standards: A1.F-IF 2 Use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context.

Honors Math Lesson Sequence:

1. I gave the students two problems in which they had to substitute a value for f(x) and then solve for x. I did not give instruction initially and had two different pairs of students put their solutions on the board. I then had a random classmate critique the work. Both pairs of students were successful in putting the problem on the board and the person critiquing recognized it. 
2. From there, we did a second problem. I had assessed about half the class already by circumventing the room and also seeing and hearing the work of the five students above. I wanted to solidify the concept though. It seemed like students were able to wrap their heads around substation for the output in order to discover the input. 
3. QSSQ. As part of the question of the day, I also revisited some of the questions that were asked during our Desmos lesson the previous class. I communicated that we need to stay within the framework of math vocabulary based questions and resist the urge to say "Is your graph in the top row?" or "Is the line blue?"  
4. We played pepper with function notation. Again through the auditory responses that I was receiving it was apparent that students were able to use function notation correctly. 
5. Students began the homework with about twenty minutes left in class. I really liked the questions that were created for this assignment and the students found them challenging as well. Particularly the one about the function relating the number of students to the cost of a field trip. 

Day 46 Desmos to the Rescue

Regular Math Objective: Find unknown triangle side lengths by applying the Pythagorean Theorem; Apply the Pythagorean Theorem in the coordinate plane

Regular Math Standards: 8.G. 6a. Understand the relationship among the sides of a right triangle. b. Analyze and justify the Pythagorean Theorem and its converse using pictures, diagrams, narratives, or models.
8.EE.7 Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
8.EE.8 Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.

Regular Math Lesson Sequence:

1. QSSQ
2. Take the quiz
3. TenMarks or Retakes 

We're getting there with this standard. The rational number is correctly converted. The repetend is in a good spot. The student is putting a zero to extend the terminating decimals and make the thousandths spot relevant for the repeating decimal. And yet it was still in the wrong spot on the number line. I'm an angry little math teacher for giving no credit on this, but so is the standardized test. 

Not pictured in this picture because I'm not a photographer is the fact that the student drew a right triangle off to the side to help with this question. And yet the right angle was left off. Again, we're making some progress.

Despite struggles with other questions, students were writing the formula for this one. Many did not have the number sense to get the square root of 169, but that's not something that just happens with one unit of Pythagorean Theorem. We will continue to hammer basic facts through TenMarks and Pepper.

Honors Math Objective: Identify function notation and differentiate between the input and output in function notation

Honors Math Standards: A1.F-IF 2 Use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context.

Honors Math Lesson Sequence:

1. Before students entered my room I read them the riot act about complaining and their work ethic. It was the first class of the morning. Everyone loves to be miserable first thing in the morning, but I had to set a tone before they did. The group is a great group individually, but culturally a few complainers are spreading a culture of whining to the entire class. We've done some really challenging things in class especially surrounding absolute value, but after looking at their exit tickets the previous class some of the kids are just complaining to fit in. I asked a handful of students publicly if they knew their vocabulary. I had given them the words and definitions more than a week ago. And there weren't 65 terms. It was about ten terms. "Most of them." Most of them! That's not good enough. How much time do you spend on homework? "Some days 15 minutes. Some days no time." And you can't get all of your vocabulary?!
2. As a warm up students tried to solve a 3 x 3 magic square. They had some success and it was a true Goldilocks Task. I only gave it out because we did it in Math Academy that morning. 
3. Homework review and pepper.
4. Desmos. We did the linear functions polygraph activity (it's basically guess who with linear functions). I was apprehensive going in because I had never used Desmos before. I had several backup plans warming in the bullpen. Their TenMarks weekly quiz for next week was ready. We could look more in depth at Pythagorean Theorem since regular math was the only class to do this. Clayton Kershaw was on full rest. None of them needed to come in though. In fact when I hit pause with five minutes to go to give a similar exit ticket to the previous day. My complainers were complaining that they wanted to keep playing. 

Here was some of the math dialogue that got recorded:

• Does your line cross through the origin?
• Does your line pass through quadrant 1? 
• Is your line a function? 
• Is your line increasing or decreasing? 
• Is the slope positive?
• Are all the x-coordinates on your graph positive? 

Then there were some questions that demonstrated some mathematical gaps:

• Is your line diagonal?
• Is it a short line? 
• Is there a tilt in the line? 

I also saw some questions that were well...

• Have you heard the Pina Colada song? 
• Do you enjoy Cheez-Its?
• Is your line blue?