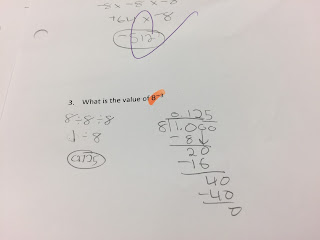Day 22: TenMarks Procedures Rehearsed

Regular Math Lesson Objective: Rewrite and solve exponent expressions that raise a power to a power

Regular Math Standard: 8.EE.1 Know and apply the properties of integer exponents to generate equivalent numerical expressions. 

Regular Math Lesson Sequence:

1. Which One Doesn't Belong (1, 9, 36, and 45)
2. Logged into Chromebook and did a TenMarks rounding decimals lesson 
3. Had four students do problems from the homework on the board 
4. Did a quick exponent power of a power exploration (which I skipped in one class due to time constraints)
5. Exit Ticket. This consisted of three things. First, rewrite (5^2)^4 in expanded form. Second take that same expression and put it into exponential form. Third, rewrite the expression 7^6/7^3 and then write it in standard form. 

Only one class needed to be prompted to bring up the perfect squares and rational numbers with Which One Doesn't Belong. It was refreshing to hear students also talk about composite numbers and divisibility. 

Some students really struggled with rounding on the computer. I was not surprised given how difficult it can be to do problems on computers and given what I know from teaching sixth grade surrounding place value and rounding. My colleague and I discussed how there is just too much on the plate for these students in math now. I can only remember working on the operations, fractions, and place value when I was in elementary school. Today there is so much more that they have to know and as a result their mastery of what I would perceive to be the basics is no longer a guarantee. 

The power of a power exercise was good once my co-teacher told me to write (3^2)^4 as 3^2 x 3^2 x 3^2 s 3^2. I was initially writing out three eight times to explain this to kids. The tickets to leave were pretty on target. As the pictures below illustrate some students made errors in putting the exponent (one student used 6 and another used 9) on problem two, but overall they are seeing the big picture. 

Honors Math Objective: Solve addition and subtraction inequalities

Honors Math Standard: A1-REI-D12 Graph the solutions of a linear inequality in two variables as a half-plane (excluding the boundary in the case of a strict inequality), and graph the solution set of a system of linear inequalities in two variables as the intersection of the corresponding half-planes.

Honors Math Lesson Sequence:

1. Which One Doesn't Belong (x squared, 4 - 2y, x - 1, and 3 (x + 1)
2. Login to TenMarks and complete the work on rounding decimals
3. Review the homework
4. Exit Ticket on inequalities

There was a great question about an absolute value equation in the form of c |x - 4| + d = e where a student asked if we could divide by c before subtracting by d on the homework. We went through what could be done in this scenario to make sure that c/d was a fraction if you did divide by c. I honestly had never really considered doing the division as I had been trained away from this at a young age and never thought to question it. It was enlightening for me to learn too. 

The which one doesn't belong is a great conversation about what it means to simplify because students could argue that 4 - 2y can be simplified and so can 3 (x + 1). 

The exit ticket went pretty well for the most part. From what I can tell students know what they are doing with the inequalities. It is subtracting by a negative or subtracting from a negative that threw them off if anything threw them off. Only one student left the dot open when graphing. 

Day 21: Flipping the Inequality Sign

Regular Math Lesson Objective: Multiply two different exponents with the same base; simplify division exponential expressions by factoring

Regular Math Standard: 8.EE.1 Know and apply the properties of integer exponents to generate equivalent numerical expressions. 

Regular Math Lesson Sequence:

1. Chart with the base of 3 for a warm up
2. Review the homework and pepper
3. Students worked on an exploration to match the objective of dividing exponential expressions by factoring. It was really helpful to see students write the word factor as part of their reasoning to the first question on the exploration about how to simple 8/12 and 2/3. Interestingly many students claimed that 2 to the 7th power over 2 to the 5th power in expanded form could be simplified because the numerator and denominator shared a common factor of 4. When they said this, I crossed out a 2 times 2 on the top and bottom. It became more apparent that we could cross out more. 
4. Passed out progress reports for students to have signed 
5. Exit ticket to assess student knowledge of the lesson and the previous lessons. 

The above image is the first of three questions I asked of students on the exit ticket. Overall, I was pleased with the work that students showed. This is the fourth different base that they have seen in four days (base 2, base 10, and base 3) so I think it's clear that the repetition is making an impact. As the picture above illustrates, students were not writing 1/4x4 in expanded form, so I put the feedback directly on the exit ticket for these students. 

This was the second question that I assessed. The top error is something that I did not see a whole bunch of times, but I thought the misconception was worth showing here. My writing is the red ink for the student who added the exponents. The lower picture is a great reason for why students can find simplifying these expressions valuable. It saves a tremendous amount of labor.

The last question pictured above is going to be covered by the next day's lesson, but many students put together quality answers. I had several state that 3 to the second power to the fourth power was 81 squared. I also had students do what was done above. It's amazing how when one thing is taught to them all day that they become fixated on that being the pathway to solve all problems. It's this type of thinking that  is forcing me to be less willing to give answers immediately to students this school year instead of letting them explore first.

Honors Math Objective:

Honors Math Standard: A1-REI-D12 Graph the solutions of a linear inequality in two variables as a half-plane (excluding the boundary in the case of a strict inequality), and graph the solution set of a system of linear inequalities in two variables as the intersection of the corresponding half-planes.

Honors Math Lesson Sequence:

1. Open Middle - Creating an inequality using the integers -4 to 4 to get x > 2/3. I was a little disappointed with the class on this problem. They immediately expressed frustration and became defeated just at the site of the task. Only two of the seven or so groups in the room made an honest effort to attack the problem. And while I will freely admit that this problem is a challenging problem, it is also a seventh grade standard being taught to eighth grade students. It could be that student confidence is low in this class after the most recent quiz and that is having an impact. I think the kids got the message when I asked how many students had bothered to write the integers from negative four to positive four in a list. Only three out of twenty-six hands went up to indicate they had done this. The kids had no objection when I said that even if they had no clue how to solve this they should have at least taken this step of writing what they do know. I would one hundred percent use this problem again in the future - to not use it would be watering down the class.
2. Passed out progress as students worked on the warm up problem to be signed.
3. I had the students do addition and subtraction inequalities in their groups while I circumvented the room. I have basically ditched the concept of taking notes this year and find that student engagement is higher and that I can clarify issues better in this way. Students are also doing more thinking. To save me some aggravation, I had the students repeat after me that it was not homework (since it said it at the top). 
4. I assigned a similar homework to the sheet above to ensure that students were getting independent practice to what they had peer assistance for during class. 

Day 20: Exponent Charts

Regular Math Lesson Objective: Create a chart with comparisons to standard form, expanded form, and exponential form with positive and negative exponents

Regular Math Standard: 8.EE.1 Know and apply the properties of integer exponents to generate equivalent numerical expressions. 

Regular Math Lesson Sequence:

1. Warm up problem was essentially the objective. Pictures are below. Overall this really clarified the errors that were seen on the tickets to leave and students were able to acknowledge that negative exponents did not lead to negative values (picture below). 
2. QSSQ
3. Students logged into TenMarks for the first time. This whole process takes a long time because it takes forever to students to get their Chromebooks out of the Chromebook cart. Every minute counts when class is only 23 minutes on half-days. 

Honors Math Objective: Dependent on what the students did in class

Honors Math Standard: Dependent on what the students did in class

Honors Math Lesson Sequence:

1. Students login to TenMarks. I had one student call out which students should be taking a Chromebook as this was taking place so that I could pass back exit tickets from the previous class. Again every minute mattered this day - although this was the long block at 40 minutes. After students logged into TenMarks successfully, I gave them a choice among three things.
2. Weekly Quiz (this was choice number one)
3. Quiz Retakes
4. Visual Pattern number 3 to Step 199. One student solved this in a unique way by adding the numbers 1 through 25, 26 through 50, 51 through 75, and 76 through 99. She then just multiplied those sums by two and added all the hundreds. 
5. Pass out textbooks for students to take home as a resource.  

Day 18: Negative Exponent Exploration

Quote of the Day: “Average performers believe their errors were caused by factors outside their control: My opponent got lucky; the task was too hard; I just don’t have any natural ability for this. Top performers, by contrast, believe they are responsible for their errors.” - Geoff Colvin

Question of the Day: How do we do the distributive property?

Regular Math Lesson Objective: Solve expressions with exponents

Regular Math Sequence:

1. Self-Assessments completed as students reviewed their quizzes in groups. I had to really prompt groups to work together to help students that got problems wrong. Rather than saying out loud "go over this with your groups" I literally had to go to a kid in a group and ask them what the correct answer for a certain problem was. When they were lacking confidence I looked at someone else in their group of four who had the correct answer and said "ask them." I wish this was not the case, but for some reason (maybe it's insecurity maybe it's lack of executive function) this sort of prompting is necessary. 
2. QSSQ
3. I reviewed whatever was left for going over quizzes after groups had a chance to review together
4. Exponent exploration to find exponents with positive bases and negative exponents. I derived this from an Illustrations discussion about how students arrived at negative exponents. I messed up question four slightly and have since fix it to say that the two bases are opposites not the two exponents. I really enjoyed this packet because it served as a great way to activate prior knowledge for the lower students especially and it was clear that the high students benefitted because nobody that I could see correctly labeled 2 to the 0 power, 2 to the negative 1, and so on. Students were saying of course that 2 to the 0 was 1. 
5. Exponent exit ticket. Most students were able to find 8 to the third power (as I would hope) and -8 to the third power (I was not as sure on that one). Nobody could find 8 to the negative third. I told them to really think about this one and challenged them throughout the day by stating that nobody had been able to do it. Most of the answers I saw were either -512 or 512. There were some other creative answers.

Question of the Day: How do we know if there will only be one solution in an absolute value equation?

Honors Math Lesson Objective: Graph and write inequalities

Honors Math Sequence:

1. Pass back quizzes and do a self assessment. 
2. Review the quizzes (it only took 40 minutes!)
3. Exploration with inequalities (Big Ideas generated) 

The review of the quizzes felt therapeutic. I had many students get below a grade that is their expectation for themselves, so I told them things were rainbows and puppy dogs, and told them to focus on the math. 

The inequalities work was much briefer than I would have liked, but we did at least get to graph a couple and write a couple. It seems like the students feel comfortable with the whole process, but I'll begin tomorrow with what was supposed to be today's exit ticket. 

Day 16 & 17: Absolute Value Study Guide & Quiz

Regular Math Lesson Standards: 8.NS.A.1Know that numbers that are not rational are called irrational. Understand informally that every number has a decimal expansion. For rational numbers show that the decimal expansion repeats eventually, and convert a decimal expansion which repeats eventually into a rational number. 

8.NS.A.2 Use rational approximations of irrational numbers to compare the size of irrational numbers, locate them approximately on a number line diagram, and estimate the value of expressions (e.g., 2). 

Regular Math Lesson Objective: Approximate irrational and rational numbers on a number line; Turn repeating decimals into fractions

Regular Math Lesson Sequence:

Study Guide Day

1. Study guide done individually
2. Fix weekly quiz highlighted problems when done the study guide
3. Find the approximate square roots for every number from 1 through 40 with fraction approximations and decimals using a calculator

A handful of students answered every study guide question correctly. In those cases, I let them skip taking the quiz and just gave them a 100 since the study guide is the same as the quiz. What I was really trying to accomplish by having the students do the study guide individually was to give them an honest feel for what stood between them and mastery of the content. I was hoping that in recognizing where they were short in their understanding they could make up for the deficit through effort and my feedback. I did go up and down rows as well as my co-teacher when he was with me to try to do our part.

The one part of this lesson that I particularly enjoyed was in my last block. As I was going over the study guide with the students I sensed I was losing them. Rather than pressing on I called students up one question at a time to show us how it was solved. I was talking less and was able to narrow my distance between students as a result which increased focus. It's something that I will do going forward in reviewing the study guide - even if it means that time will not allow me to finish reviewing.

Quiz

1. Take the quiz
2. Do the new WQ 
3. Do 3 Sheep, 5 Wolves 

Here were some positive outcomes from the quiz:

This chart was made by a student after I recommended it to him the previous day. He did it without any prompting. I think it makes it much easier to grasp where irrational square roots will approximate to. 

This was another extra piece provided by a student. I had asked for the numbers that are next to the letters to go on a number line. This student decided to convert them immediately to approximations and then put them on the number line. It is encouraging to see that the approximate signs are all used correctly and the equal signs are used correctly. 

Here are some signs that we have some work to do, but overall there is reason for optimism. 

The student on problem 6 could correctly place the denominator as being the distance between the two perfect squares and also put 5 as the whole number. We just need to interpret what the 6 means in this problem. 

In problem 9, the only thing that went wrong was that the student subtracted 10 from 1000 and got 900. In my opinion this was more of a rote error (they've memorized a process) than a math error (they are not asking if the answer makes sense). 

Honors Math Objective: Find the values of x for an absolute value equation; explain why some absolute value equations have no solution; eliminate extraneous solutions from an absolute value equation

Honors Math Lesson Sequence:

Study Guide Day

1. Study Guide in partners
2. Review homework question regarding what happens if an absolute value equation is 0, negative and positive
3. Continue to work on the study guide in partners 

The study guide was not finished at the end of class because the issue of determining how negative, positive, and zero set equal to absolute value brackets took up a huge amount of time. This question to me is imperative for mastery of absolute value, so I'm not sure I would do it much differently in terms of what gets done. Perhaps this question though could have been duplicated onto the study guide so it became something that students were collaborating on in addition to doing it individually for homework before we went over it as a large group. 

As a partial result of not completing the study guide, I think students failed to reach their potential on this quiz. I also think that there are other errors that I have elaborated on in Days 13, 14, and 15. 

Quiz Day

1. Take the quiz 
2. Five Wolves, 3 Sheep

The errors on the quiz were numerous. That's what happens when the teacher does not facilitate the instruction as it should be. I will tell the students this as well. The last thing I want them to do is panic because I made mistakes. They will have opportunities to retake this quiz and I am going to go over the quiz in detail on Monday to help begin the clean up. 

In the top problem, the student did everything correct. The only thing missing was the entire concept that there should be a second solution. 

In the bottom problem, again the student did everything right including finding both solutions. The student made the mistake though of saying that both numbers were not solutions for some reason. 

Both of these pics illustrate a popular error I noticed. Students quickly dismissed this problem because of the negative sign as the pictures indicate. 

There is still work to be done. Tomorrow with going over the quiz I spent two hours creating a SMART Notebook review. Hopefully I can be just a facilitator, but it is proving to be a challenge with absolute value. 

Day 15: Radical Expressions

Regular Math Lesson Objective: Estimate radical expressions for which an irrational number is present; solve radical expression for which perfect squares are present

Regular Math Sequence:

1. Open Middle Warm Up as I collected the weekly quizzes
2. Review Open Middle and homework
3. Do one problem where students have to find the value of an expression with a perfect square and review on the board
4. Do one problem in which students have to find the value of an expression with an irrational square root and review on the board
5. Give an exit ticket

As the exit ticket indicates, students could solve an expression for which a perfect square is given. It was more difficult for them to do it with an irrational square root. The student on the left mistook the idea of square root to mean two times a number equals 15. The student on the right demonstrated higher thinking by writing out the perfect squares that were on either side of the square root of 15 (9 and 16). And while I would rather that student just use 4 to approximate the value of 15 since it is a better approximation than 3.5, 3.5 is at least in the neighborhood.

I think for some students they have to be in the habit of writing out __ x __ = 15 to prompt the thinking about square roots as opposed to what times two equals that number because it has been the most common misconception that I have found with students. I also believe that by writing out the neighboring perfect squares, students are having more success.

Honors Math Objective: Solve absolute value equations

Honors Math Lesson Sequence:

1. Visual Patterns #3 as I collected the weekly quiz
2. Review the homework 
3. Continue working on the four problems from the previous class
4. Start tonight's homework in class

As a result of students working in groups, the students were in very different parts of this assignment. Originally I would not have guessed that they would be able to begin the homework, but that ended up being the case since some groups finished well ahead of others. This was not due to classroom management issues, but rather students were struggling through the problems while others were having less resistance. 

Where this lesson was lacking was my inability to give an exit ticket. I should have seen just what students were capable of without classmates helping them or homework answers from PedrothePig (class website) in front of them.

Day 14: Absolute Value & Negative Solutions

Regular Math Lesson Objective: Estimate square roots of irrational numbers

Lesson Sequence for Regular Math:

1. Jumpstart (Open Middle Rational and Irrational Square Roots) 
2. QSSQ
3. Review the homework and pepper
4. Irrational Estimation Practice
5. Exit Ticket

Glass Half-Full: The Open Middle problem in the jumpstart hit the spot. It was a goldilocks task (not too easy but not too hard) and enabled me to go around the room to assess homework and pass back weekly quizzes and exit tickets from the previous class. With specific kids I was able to give direct feedback. It was also useful to have the students working in groups of four for this task to bounce ideas off of each other and clarify what they were expected to do.

Regrets: The irrational estimation practice was well done by the students on the front side, but on the back side they again had trouble in the same area that they had trouble the previous day. I think if I were to do this again next year, I would have made the irrational estimation practice an assignment for Day 13 and the Illuminations activity the focus of this day's lesson. That way students had a foundation for recognizing at least the whole number portion of where the number came from.

Exit Ticket: The students were proficient in determining what numbers a square root was between and also what whole number it would be closer to.

This student successfully could obtain the numerator and denominator. One thing that I wish I had put a higher emphasis on was the approximate sign to help students recognize that everything we were doing to estimate was centered around the fact that getting to an exact number was impossible since these were irrational numbers. I also wish that I had suggested students could guess and check or draw pictures if necessary.

Lesson Objective Honors Math: Discover extraneous solutions to an absolute value equation

Lesson Sequence for Honors Math:

1. My Favorite No 
2. QSSQ 
3. Analyzing my favorite no 
4. Four multiple step absolute value equation problems in groups of four

My favorite no was appropriately paced and students were able to discover the flaw in the problem with high success without any instruction. 

We then launched this into a problem with an extraneous solution. And this was a bit more of a struggle because students still were unable to derive the fact that there should be two solutions and failed to write two separate linear equations. Instead these students wrote just the one. 

In terms of the last part of the lesson, it was inappropriately paced. Students really struggled with the first problem which was | 3x - 10| - 10 = -4

I had three other problems also on the board. I feel like if they were able to do just that one problem that they would have had significantly less issues with the other three. The greatest struggle that I have is that I am making a huge effort to stop giving students answers. The students and the teacher are not used to it, but in reality I think it is what's best for them. I had one student ask me if the minus ten in absolute value brackets cancels out the minus ten outside the brackets since the minus ten in brackets is going to be positive. I told her to try it and see if the solution matches the original equation.

The thing that makes all of this so difficult is that there is only fifty minutes. Discovering and staying with it can take me for a loop for over an hour at times and we also did the whole my favorite no shenanigans which took up half the class. If I were to revise it, I would place only that one problem on the board so that we could discuss what different students did and narrow our focus a little more. 

Day 13: Irrational Square Roots

Regular Math Lesson Sequence:

1. We made a perfect square chart for the first ten counting numbers 
2. We took notes on perfect squares using the square roots go rational task from Illuminations 
3. We did a couple problems including the square root of seven and the square root of 32. 
4. The students did an exit ticket finding the square root of 10. 

While this exit ticket demonstrates precisely what I would like the students to have obtained from the lesson, there were more signs of weakness than strength on the exit ticket so I will go back and tackle this lesson with more emphasis on finding the perfect squares that an irrational number sits between. 

Honors Math Lesson Sequence:

1. My Favorite No: The absolute value of | x + 2 | = 3
2. Reviewing the My Favorite No
3. Exploration from Big Ideas textbook. The students had to find the absolute value by getting two linear equations, using a number line, and doing a t-chart. 
4. Pass out that night's homework

The My Favorite No was not answered correctly by a single student. Most students put x = 1 and only one wrote -5, but even that student did not have 1. As students were passing it in they were skeptical that it should be harder than simply recognizing that 1 was the value for x. 

As students were doing the exploration in Step 3, I realized I was not the biggest fan of it. The t-chart was a lengthy way of solving it. And if fraction solutions were included it was only longer. The other way of a number line was useful, but probably something that could be put off for another lesson when teaching students how to solve for a minimum and maximum. I say this all in hindsight of writing after the quiz was given in which none of the students utilized a t-chart or a number line (with the possible exception of a midpoint problem). 

Where today could have been more valuable is discussing why two linear equations were appropriate and why the negative and positive versions of what was to the write of the equal sign was the only thing that differentiated between those linear equations. It also would have been helpful to show students that checking the work is done by plugging in each solution for the variable into the original absolute value equation instead of the positive and negative versions of the linear equation. 

Day 12: Reflecting on Quizzes

Quote of the Day: “Punishment is for the punisher’s benefit, to make him or her feel better. Discipline always has the other person’s best interest in mind.” - Helen Williams

Question of the Day: Any questions that the students had on the quiz. Especially where to find a repeating decimal on a number line.

Lesson Objective: Discover what numbers can be perfect squares

Lesson Sequence:

1. QSSQ
2. I passed out manilla folders, quiz self-assessment sheets, and yesterdays quizzes to all students. The manilla folders are used to store the students self-assessment checklists all year. That makes it easy for me to determine where students need to be retaught and retested (not always in that order).  
3. The students discussed the quizzes in groups. 
4. I passed out a paper copy of the weekly quiz and reviewed for students the expectations of it. 
5. I gave students 40 tiles that were cut out to be about 1 inch by 1 inch. This was the sheet that they used to discuss square roots in their groups. At some point between questions 6 and 8, we crossed into the lesson objective. One particular class had a great discussion about the fact that it was possible to find two of the exact same numbers to get an area of 40 for a square. 

Glass Half-Full: The glass-half full could fit for both classes. Having students discuss their quizzes the day after it is graded is something that I have never tried before. In the past I would just stand and deliver as students either asked me questions or I would simply generate a list of problems to review based on grading the papers the night before. I was afraid to let students review in groups because I did not want them to feel insecure or embarrassed if they did not do as well. To help alleviate that concern, I left the grades off the top of the papers. Students were forced to calculate their own grades based on how many questions were right and wrong. In essence it took the focus away from a number that would seem arbitrary to them and put the focus on where they were short in their learning.

In reality as I told the students, despite all of my pleas to have the students keep their grades private after quizzes and tests throughout my teaching career, I was still often ignored. Some students would just shout out "I knew I failed" or "I got a 100!" Other students would ask the people around them "Whadya get?" and before I could condone them the answer had already been given. And still others would simply peak to their left or right and easily make out the red X's. Today, I told students to let me know if they were uncomfortable having their peers know how many questions they got wrong. So far I have not heard anything negative about the process from anyone.

All in all, I think this process of reviewing a quiz was much more productive than in the past with standing and delivering. I was able to circumvent the room and confront the difficulties of students that might tune me out if I was speaking to the larger audience. These students also asked me follow up questions one on one where in the larger group they would simply nod their head out of fear for being in the spotlight. The students who were doing the teaching were of course gaining a deeper understanding having to explain to classmates who might be probing with more why questions than they might otherwise receive. And they also were more engaged than they would be if I was simply re-explaining something that they already understood.

Honors Objective: Analyze the value of two different variables in relation to their absolute value given that one number is negative and one is positive

Honors Lesson Sequence: Same as above with the exception of the fifth item on the agenda. This was changed to a task from the Big Ideas book. Students worked in groups determining what happened with negative signs outside and/or inside of absolute value brackets as well as changing inequality symbols to determine sometimes, always, and never as well what set of integers proved the inequality true.

Regrets: This goes with both classes (as does the glass half-full outlook). I wanted students to reflect on how they did with their quizzes as it related to their action steps leading up to it. Here is a summation of probably half of the responses I received:

These ones below were more in line with what I was hoping to get. They are honest. They are points that I can at least work with going forward. And in fairness, sometimes paying attention is enough to be more than effective. 

Finally these responses were more elaborate and specific. I like how the students named off the actual skills that were required of them, mentioned something along the lines of their learning style, and specific actions that were taken instead of just "study." The challenge for me of course is that some students do not know their learning style, have never been taught how to study, and if they did not do well on the quiz why would they know what topics were covered? Theses responses were few and far between, but serve as good exemplars to show the rest of the student body in terms of how reflective I want them to be and more importantly what type of students I want them to become. 

Days 10 & 11: Number Sense Study Guide & Quiz

Quote of the Day: “You should be willing to do something that will take you five minutes or less for anybody.” - Daniel Rifkin

“The formula is 6-2-7; breathe in for 6 seconds, hold for 2 and breathe out for 7 seconds.” – Jason Selk

Question of the Day: How does a number like .52 repeating get converted into a fraction?

Regular Math Lesson Objective: Convert repeated decimals to fractions; locate a fraction that repeats as a decimal on a decimal number line; Convert between terminating decimals and fractions

Lesson Sequence:

1. QSSQ
2. Review last night's homework
3. Study Guide
4. Illuminations Exit Ticket

Lesson Sequence the following day:

1. QSSQ 
2. Take the Quiz
3. Sign up for Google Classroom
4. Work on Get to 10 inside Google Classroom 

Glass Half-Full: I found myself suddenly optimistic toward the end of the study guide. I had my doubts coming in, but one way or another we needed the students to feel accountable in the gradebook. The sense of urgency picked up today and students were able to piece things together to my surprise. 

Regrets: Students are still struggling with what a rational number truly is based on the exit ticket results. I also know that we will need to continually spiral back the skill of repeating decimals to fractions because students have that processed memorized as opposed to applying logic to it. That said, I don't blame them for memorizing this skill. I asked a college friend of mine who would tutor me if he could turn a repeating decimal to a fraction and he said it would have to be through guess and check. It's just not something that people generally "need to know." 

Honors Math Objective: Solve multi-step equations; convert repeating decimals to fractions; approximate square roots of irrational numbers 

Lesson Sequence Honors Math: 

1. QSSQ
2. Review the homework
3. Study Guide 

Lesson Sequence the Next Day:

1. QSSQ
2. Take the Quiz
3. Sign up for Google Classroom
4. Get to 10

Glass Half-Full: Looking at the mistakes that students made, it's not as if we'll need to watch Sesame Street tomorrow. The biggest issues were locating numbers on a number line (it was the same mistake made throughout with students not using the thousandths place to help them see where to place the number). The other mistakes were on the two-step equation problems. The top answer is a student that tried to cancel a minus 7x with another minus 7x. The second example is a student that combined like terms as if they were in an expression instead of in an equation. The third example is a student that is not correctly distributing the sign with the 7x. I will address all of these in going over the quiz and also encourage these students to retake the quiz since they are missing only a very small piece of what is needed to reach full success. 

Day 9: Going Irrational

Quote of the Day: “Let’s face it. This is the relationship age! The information age is over - there is too much of it, everyone has access to it, and much of it is not useful. Your success depends on the quality of your relationships.” - Greg Bell

Question of the Day: What is 0.16 with the 6 repeating times 100?

Regular Math Objective: Convert a repeating decimal to a fraction.

Regular Math Lesson Sequence:

1. QSSQ (I skipped the question part until after the number talk)
2. Number talk. 94 - 49. I had the students do a reflection in each class. I simply had them write down how many times that they have participated by either giving an answer, a strategy, asking a question of one classmate, or opening up a discussion for the entire class. I then had them make a goal of how many times they would participate in our next two number talks. In two out of four classes it had virtually no impact, in one there was a small impact, and in the other there was a huge impact. I think it all can be tied into social dynamics, but in any case some results are better than none. Some students are still answering it incorrectly at times, so we still have great conversations. I'm really surprised that people do not laugh at their classmates for wrong answers, but it is a complete none issue in this routine. 
3. My Favorite No. I asked a series of four questions. The first was to get students to extend 0.16 to 5 decimals places. The second was to get students to extend 0.16 with the 6 repeating to 5 decimals places. The third was for students to multiply 0.16 with the six repeating by 100. And finally I had students find x for the equation 90x = 30. The answer below was the most popular wrong answer I saw all day and I did not anticipate it at all until actually asking students to think before I spoon fed them the answer. 
   
   
   
   
   
4. After discussing popular mistakes for each of these four questions, we talk quick notes of how to go from .4 repeating to 4/9. I showed them this in five steps. First, set the repeating fraction equal to a variable. Next, multiply the variable a base ten number. We had to review what a base ten number was. In the future, it would be helpful to show students a chart with the 10s all put to different exponents. Third, students multiplied the variable by a different base number. Fourth, they found the difference between the two base ten numbers and the decimal equivalents of these values. Fifth, they solved the multiplication equation. 

Outcomes: I hate teaching in a stand and deliver mentality, so I sort of avoided. Students discovered some of the process on their own with My Favorite No. In essence it is the same thing in an ELA class as making predictions before reading to be more invested in what is being read. I also tried yesterday to get students to do this process on their own and had very limited luck and some classroom management dilemmas to confront as a result of students being over challenged. 

Overall students seemed ok with this concept. The mistake above is something that I'm barely concerned with when considering the bigger picture of everything else that needs to be done. 

On the surface this looks great. Perhaps I'm overanalyzing, but I'd be worried that this student would flop without notes and would have trouble thinking about this problem critically. What would happen for instance if the decimal was 0.121212 instead of a single repeating decimal? Could the student make the necessary changes to find the fraction equivalent? 

I have most confidence in an answer like this. The students recognizes how to simplify (which I did not ask students to do) which is nice, but they seem to recognize the entire process as one big entity rather than a series of steps. 

Honors Math Objective: Approximate square roots of irrational numbers

Lesson Sequence: 

1. QSSQ
2. We analyzed some of the pictures from the two-step equations of the previous class. I tried to boost student confidence by stating that most of their work was good. We just needed to clean up one flaws in a process that includes in some cases more than ten steps. 
3. Square Roots Go Rational. We began the discussion by looking at the distance in areas between each of the squares on this chart. One of the students pointed out that there was a distance of three numbers from 1 to 4, a distance of five numbers from 4 to 9, etc. In doing so, I then transitioned to the visual on the Illuminations lesson linked above ("Square Roots Go Rational"). I asked students to tell me how many X's were needed to go from a 3 x 3 square to a  4 x 4 square. Next, I showed them a 2 x 2 square with the X's and we discussed if I added three more X's if that would create a square. The class was quick to shoot down this notion. We had a brief discussion of rational versus irrational numbers. Then we were able to see that we had three out of five possible X's to get to the next perfect square. Using this number (2.6) we were able to approximate the square root. From there, students worked in groups of three to complete every irrational number's approximation from 1 to 40. 
4. Students did an exit ticket of the square root of 80. Intuitively they knew that it was between 8 and 9. I told students to solve it however they would like. Many of them guessed and checked. Some of them used fractions. And others drew the picture with the X's (although not all 80 X's). Overall there was solid understanding from the lesson. 

Day 8: Two Step Equation Errors

Quote of the Day: “In one of the most famous experiments in the history of psychology, Walter Mischel and his students exposed four-year-old children to a cruel dilemma. They were given a choice between a small reward (one Oreo), which they could have at any time, or a larger reward (two cookies) for which they had to wait 15 minutes under difficult conditions. They were to remain in the room alone, facing a desk with two objects a single cookie and a bell that the child could ring at any time to call in the experimenter and receive the one cookie. Ten or fifteen years later, a large gap had opened between those who had resisted temptation and those who had not. The resisters had higher measures of executive control in cognitive tasks, and especially the ability to reallocate their attention effectively. As young adults, they were less likely to take drugs. A significant difference in intellectual aptitude emerged: the children who had shown more self-control as four-year-olds had substantially higher scores on tests of intelligence.” – Daniel Kahneman

Question of the Day (from a Student): Why is it that there is a 6 out of nowhere when five is divided by six?

Lesson Objective (Regular Math): Convert repeating decimals into fractions

Lesson Sequence: I read the quote and question first.

Next was the Number Talk. The number talks have gotten better everyday, but this was to be expected. I would like to see more students participate because everyday for the past four days now has been a subtraction problem. As I said there have been improvements, so students are no longer simply using the standard algorithm. My colleague and I discussed the possibility of doing a reflection. We could get the students to answer the question how many times have I volunteered to speak out. Speaking could mean saying an answer, sharing a strategy, asking a question of a specific classmate, or asking a question to the class in general.

The next thing that we did was work on the repeating decimals to fraction algorithm. This is a challenge for most people and if I were to venture a guess I'd say more than 50% of college educated adults could not do this. Thus we struggled. That said, students successfully were able to take the decimal form of fractions as they are presented in the calculator image above and correctly remove the rounded portion of the decimal. Where the conversation baffled them was in two places. First of all, the idea that a number such as 0.16 with the six repeating (apologies on not showing that notation in Blogger) was not equivalent to 16 when multiplied by 100. For some students recognizing what happened to a number multiplied by 100 was an issue.

The second issue came when the subtraction of 100x - 10x was complete and students had to take the 90x remaining and set it equal to 15 (the difference of 16.6 repeating and 1.6 repeating). Students were doing 90 divided by 15 instead of 15 divided by 90. I was quick to ask how a number like 0.16 could be greater than one as students told me the answer was 6.

In terms of where we go from here, I think there is a certain degree of repetition that will need to be revisited here, but also getting students familiar with the various ways to write a repeating decimal and what that number looks like multiplied by various bases of 10.

Lesson Objective (Honors Math): Solve for a variable in a multiple step equation

Lesson Sequence: I read the quote and question, but accidentally skipped the number talk. It was probably for the better as the time we spent on two-step equations was valuable.

I gave students the problem 2/3p - 4 (p + 3) = -7p + 10 as a My Favorite No problem. Index cards were distributed for each student. I gave students about seven minutes to work out the problem (the students must have thought it seemed more like one minute because many were stumped). Here were some of the answers that I saw.

This was probably the most common error. As it was displayed on the board, a couple students were quick to point out the error that there should be a minus 12 instead of a plus 12. I tried to help them by stating that the distributive property is multiplication and we are really "taking away four groups of p +3." 

Here the student did almost everything perfectly until the last step. The 22 to the left of the equation was ignored and the 7p that was added to the left side at the end never got added back to the right side. Too often I am guilty of giving credit for right and no credit for wrong. Upon showing work like this to students I am not sure if that's fail. It's fair to say that the student has work to do in terms of mastering the standard, but by the same token the student can distribute correctly and also knows what is needed to balance equations. 

This is a third positive example that does not demonstrate mastery, but is certainly close to achieving that. The student writes that -12 - 10 is -2. Perhaps this is a complete misunderstanding of that concept or just a simple mistake in this one instant. How is that measured? At the end there is also some difficulty combining like terms, but this only appears to be the case with the fractional coefficient. 

After the My Favorite No, I had students work in groups of three on problems that were placed throughout the room to get them out of their seats. Through working in groups of three, they were able to get feedback on these minor issues that I might not have been able to give them if they were working individually. At the end of class I asked students what they would consider thinking about as they were doing a two-step equation to make sure they did not make a mistake that they had made earlier in class.