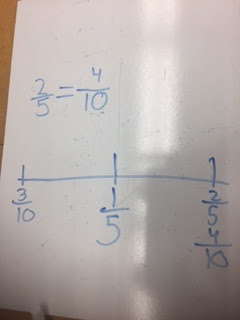Staying with the Problem: November 2016

Wednesday, November 30, 2016

Day 57: Who Wants to Be a Millionaire?

6th Grade Math Standards: 6.NS.1 Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for (2/3) ÷ (3/4) and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4 of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc .) How much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? How many 3/4-cup servings are in 2/3 of a cup of yogurt? How wide is a rectangular strip of land with length 3/4 mi and area 1/2 square mi?

Objective: Divide fractions in order to find a quotient; Place a fraction with a different denominators between two like fractions with numerators that are one apart on a number line (what fraction is between 11/3 and 12/3?)

Question of the Day: "Why is it that 3 and 4 will bring the same product and least common multiple, but 9 and 6 do not have the same product and least common multiple?"

Agenda:

Determine what fraction is between 11/3 and 12/3
Visual Pattern #32
QSSQ
Review Homework and Pepper
Who Wants to Be a Millionaire (second class). All 13 questions are going to appear on the test (students do not know this)

Assessment: The students used individual marker boards during Who Wants to Be a Millionaire; I circumvented the room for homework and pepper

Glass Half-Full: The way the timing worked out in this lesson could not have been much better. The routine of steps one through four combined with the novelty of step five in the second class was the right balance for engagement and learning to happen across many types of learners. Everything done was assessable and gave students an indication of where they were proficient and where they were lacking skills (needed reteaching or simply to cross their T's).

Regrets: I could not do all 13 questions on Who Wants to Be a Millionaire as a result of reteaching as I found student misconceptions. Ultimately, I think I would have been better off if I had strategically placed a question with each operation as well as the objective of locating fractions between number lines back to back. What ended up happening was that one class never needed to find a fraction between two like fractions and another did nothing but find a fraction between two like fractions as a result of me trying to compensate for my mistake in the first lesson. Just need to find a balance between the two and could do so by skipping around on Who Wants to Be a Millionaire rather than doing each question one by one. Students these days do not really remember how Who Wants to Be a Millionaire is supposed to be played anyway.

Day 56: Fraction Stations

Estimation 180 (Lights)
QSSQ
Stations (word problem strategies, number line, stop and think, peanut butter blossoms, WQ)
Exit Ticket (using clickers)
Start the homework

Assessment: I stayed at one group of desks and focused on the number line concept that was listed in the objective.

Glass Half-Full: The clickers exit ticket was new to this year and really helped alleviate some of my concern regarding an issue that is a chronic red x when students take the test. They are overwhelmed by the number of steps involved in these problems so I tried to keep it really simple by saying get everyone to speak the same language. In other words make them all improper or mixed and then make them all have the same denominator and then reevaluate the question.

Regrets: Not even checking in on the groups in the other stations was a huge issue because it meant that they were unaccountable. For students that lack self-discipline this meant that they essentially got nothing done. Coming off of Thanksgiving break and getting back into fractions after a five day layoff, that meant that they might be lacking the skills they need to have.

Day 55: The Brain Bowl

For the second straight year before Thanksgiving we brought the entire sixth grade together to do a "so far year in review" trivia challenge. Every student is given a TurningPoint Clicker and then given multiple choice questions from all four core subjects (science, social studies, ELA, and math) as well as pop culture and random trivia questions (who played college sports for example). The clickers keep track of score automatically for us, so the students enjoy the competitive aspect of playing for their homeroom and for their core team (either Alcott or Hawthorne in our school). After about 30 minutes, two students are then chosen from each of the ten homerooms to compete in a final round. Where we continue to give multiple choice questions and give those twenty students exposure and make all of the things that they have learned and worked hard to practice worth knowing - even if they asked, "When are we going to use this in the real world?"

I like this activity on this day for two reasons. First of all, units are being wrapped up or should be put on hold if they are not being wrapped up at this time of the year. To give an assessment on this day is hard because the classes are shortened with a half-day. If classes were to be held as if it were business as usual, the students would be unlikely to bring the same level of focus we typically see and some students are also already gone to visit grandma in Connecticut. Second, it gives the students a sense of school pride and a positive affiliation with school. This is a marathon and the enjoyment of this experience is building the appreciation of each curriculum for the students. Did we get closer to conquering the common core, getting a perfect score on PARCC, enrolling in Harvard, curing cancer, and teaching the future first president to achieve world peace and plant wheat crops on Mars? Not quite. What we did do was give students a fun memory from the year and also got a decent formative assessment for our troubles.

Friday, November 25, 2016

Day 54: Dividing by Multiplying by the Reciprocal

Open Middle find a quotient of 1/20
QSSQ
Review the homework
Reciprocals
Show students the difference between 6 divided by 2 and half of 6
Dividing by Multiplying by the reciprocal practice

Assessment: I had students stand up when they tried multiplying by the reciprocal problems on their own; checking the homework

Glass Half-Full: The open middle problem was solved by the students, but not me. I gave up after five minutes and checked the solution to see if it was as hard as I was making it. I couldn't do it without using a whole number or improper fraction cause my brain was on Thanksgiving. When I saw the answers, I saw that I might not be qualified to teach mathematics since I gave up and since it was very very easy. When the students were able to do the problem with pretty high efficiency, it was confirmed that I should be thankful that I have a job because at times they could definitely take the mic from me.

Regrets: When students stood up, they had the correct answer, but were still finding a common denominator. Is there anything wrong with that? To me, this is one of those situations where maybe adding a tool to the toolbox is not a big deal.

Link: The most fun cities. Just for the record I've been to 7 of the best 10 and 4 of the best 5.

Day 53: Dividing Fractions with a Common Denominator

Visual Pattern #27
QSSQ
Division of Fractions Intro. You and three friends get a pizza (I display a pizza on the board). Then I tell kids to look at the back wall to see what's different. When they turn around, I've changed the board to show that one slice is missing and your brother took it. They fell for the oldest trick in the book. Now how are we going to split the pizza with 7 slices (7/8 of a pie) among 4 people?
Think, pair, share
Review how to divide fractions by finding a common denominator
Notes including a number line
Independent practice and homework

Assessment:

Glass Half-Full: I found this helpful link about dividing fractions from Republic of Math about 20 minutes before school and wanted to incorporate it somehow into the lesson. I thought it was a useful of thinking about the problems and technically the standard does use the term visual fraction model. I doubt most students found it helpful, but there were probably a few, and I'm teaching "what I'm supposed to."

I have never taught students by making them find a common denominator first. The thought occurred to me in the moment when students were solving the activator problem with the pizza that most of them were in essence trying to either split the pizza into thirty-seconds or making sure each person got 1.75 slices. I don't think that students were making any connection to multiplying by a reciprocal. That was only brought about as a result of memorization. As the above link does delve into the students could eventually learn about multiplication of the reciprocal through self-discovery, but it's usually not the first maneuver students go to. Plus when we start talking about integrating the other operations, it's less for students to be confused by.
Just find a stupid common denominator. Even if you multiply. I don't care. Do it.

Regrets: I was vague as to whether students needed to find the number of slices per person or the fraction of the whole pizza per person. The two questions are different, so it would be best to ask both on the same slide. More students determined 1.75 slices per person than 7/32 of a pizza per person.

Link: Good way to practice coordinate plane and celebrate Black Friday from Robert Kaplinsky.

Day 52: Why 4 and 1/3 Times 2/5 Isn't 4 and 2/15

Which one doesn't belong?
QSSQ
Review the homework
Exit Ticket on why 4 and 1/3 times 2/5 does not equal 4 and 2/15
Mashed Potato Recipes from Yummy Math

Assessment: The homework was assessed to see students comfort level in cross reducing. Some students were on the fence as to how cross reducing would make life simpler and not more complicated. There was the exit ticket (the subject of the amount of liquid in the glass) and the mashed potato recipes were collected by me to see where students were on old concepts integrated with new concepts.

Glass Half-Full: About 83% of the students had something logical to say about the exit ticket. I think it helped that it was connected to the question of the day as well.

Regrets: The mashed potato exercise was good, but there was no time to review the results. I even gave them the answer to problem one. Somehow we have to do a better job of time management because it would have been good to review for the whole crew after collecting the work and seeing the various misconceptions and multiple points of entry for those that did solve.

Here the student triples the ingredients when the number of people to serve was not tripled.

Here the student correctly changes the ingredient, but the denominators in each picture are different.

Link: Many of the ideas in this blog post about 16 Ideas for Student Projects Using Google Docs, Slides, and Forms I was familiar with, but I thought a cool add on for my curriculum was to have students create their own form and have classmates answer it when we do statistical questions.

Thursday, November 17, 2016

Day 51: Multiplying Fractions

6th Grade Math Standards: 6.NS.1 Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for (2/3) ÷ (3/4) and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4 of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc .) How much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? How many 3/4-cup servings are in 2/3 of a cup of yogurt? How wide is a rectangular strip of land with length 3/4 mi and area 1/2 square mi?

6.G.2 Find the volume of a right rectangular prism with fractional edge lengths by packing it with unit cubes of the appropriate unit fraction edge lengths, and show that the volume is the same as would be found by multiplying the edge lengths of the prism. Apply the formulas V = lwh and V = bh to find volumes of right rectangular prisms with fractional edge lengths in the context of solving real-world and mathematical problems.

Question of the Day: Tom Brday throws 8 touchdowns for every three interceptions. What is the ratio of interceptions to touchdowns?
Objective: Multiply fractions by fractions to find a product; multiply fractions by whole numbers to find a product; multiply mixed fractions to find a product

Agenda:

Self-Assessment from the addition and subtraction quiz
QSSQ
Review the Quiz
My Favorite No
Pepper
Notes
Clickers (exit ticket)
Homework started in class

Assessment: I had the students multiple 1/3 by 2/5 to see what they already knew about multiplication of fractions. In one of my classes 11 of 18 students answered 2.

During the notes, students were consistently asked to try on their own before I showed them what to do and I circumvented the room at this time. There was a popular answer of 4 and 1/3 times 2/5 being 4 and 2/15. That was such an issue that it is going to become the question of the day for tomorrow.

The clickers were only used for one class. I had a two step problem that required students to add and subtract fractions as well as multiply them.

Glass Half-Full: As the 6th grade standards above indicate, there is nothing that is directly saying that students need to multiply fractions. It is a fifth grade standard. They do have to build upon their knowledge of multiplying though in order to find volumes and make sense of dividing fractions. So the novice in me would say let's just go right to division. The novice in me died a few years ago. When 11/18 of students answer a question wrong, there is a fraction problem (pun intended). Today's lesson was necessary, and hopefully impacted the students recognition of how to carry out the algorithm.

Regrets: The notes are designed to show students why a fraction times a fraction cannot equal two or anything greater than one. It was put in there, but once the robots - I mean students - start to multiply the numerator by the numerator and the denominator by the denominator, they lose site of this concept.

Link: Lost at School was a valuable read for me (although it took me two months to finish because I'm a horrible reader at busy times) in terms of classroom discipline. I think it confirmed many things for me and also showed me that repeated disciplinary actions are cause to change the way you see a problem in the classroom.

Day 50: Fractions Quiz

6th Grade Math Standards: 3.NF.3, 4.NF.2, 5.NF.1

Objective: Add and subtract fractions with like and unlike denominators; apply fraction operations in a real-world context

Agenda:

Marker Boards Collaboration
QSSQ
Take the Quiz
Work on Weekly Quiz, do retakes, or read

Assessment: The marker boards and the quiz

I had students each do a problem that forced them to borrow (if that was the method they were comfortable with) to get a difference with unlike denominators. Each student in a group of four did one problem like the two below.

When done they added their four differences. Again using whatever method they were comfortable with. Here one group is using improper fractions and another is using mixed numbers (incorrectly).

If they got the answer wrong of the sum of all four problems I just said wrong. I tried to stay away from explaining and left it up to the group to correct until they had what is seen below.

Glass Half-Full: Typically I give the quiz in the first 50 minutes of class and if there are students who need to finish, they can work on it in the second 50 minutes. Today I knew the quiz would not take as long. As a result we did not start the class with the quiz. Each kid was given their own marker board and told to do four separate subtraction problems with unlike denominators in which they would need to borrow (if borrowing was their preferred method of solving). Then when each student got their difference they found a sum of their four answers. I had to say almost nothing after explaining the task and students collaboratively worked out their errors. The whole task took roughly 30 minutes per class. It left me feeling like the students were prepared for the quiz.

Regrets: I think that some students are taking too long on quizzes. The fact that we needed over an hour to do this type of quiz is alarming. I promote persistence and Einstein's quote of "It's not that I'm so smart, I just stay with the problem longer." I also have to have my students prepare to take PARCC.

Link: Article for the National Council of Teachers of Mathematics on 13 "rules" that may not be helping our students.

Tuesday, November 15, 2016

Day 49: Unlike Denominators & Borrowing

6th Grade Math Standards: 3.NF.3 Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size. a. Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line. b. Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3. Explain why the fractions are equivalent, e.g., by using a visual fraction model. c. Express whole numbers as fractions, and recognize fractions that are equivalent to whole numbers. Examples: Express 3 in the form 3 = 3/1; recognize that 6/1 = 6; locate 4/4 and 1 at the same point of a number line diagram. d. Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.

4.NF.2 Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model

5.NF.1 Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators. For example, 2/3 + 5/4 = 8/12 + 15/12 = 23/12 . (In general, a/b + c/d = (ad + bc) /bd.)

Objective: Add fractions with like and unlike denominators; Find the difference in a mixed number problem such that the fractional part of the number being subtracted by is smaller than the fractional part that is subtracting from the bigger number

Agenda:

Open Middle Equivalent Fractions
Quote, Star Student, Question
Study Guide in Partners
Review of Study Guide
5 Minutes of Pepper
Independent Study Guide

Assessment: I was circumventing the room throughout the study guide. As students struggled with borrowing, I would continue to provide them with borrowing types of questions until they had successfully met the objective.

Glass Half-Full: For being a 4th grade open middle question, the warm up problem definitely made us sweat. That being said, all of my students were able to access the problem and try it. They just did not immediately come to a conclusion about its solution. In one class, a few of the students that did answer it were students that have had their share of struggles in math this year. Meanwhile students that are typically asking to be challenged or need to be challenged were still working it out. It was kind of a nice self-esteem boost for these students.

Regrets: Not having computer access hurt this lesson a little. If students could check their answer themselves or at least plug their answers into a computer in which I could oversee everything it would have been more efficient for giving feedback.

Link: I think Twitter makes sense too.

Friday, November 11, 2016

Day 48: Adding and Subtracting Unlike Fractions

6th Grade Math Standards: 4.NF.3 Understand a fraction a/b with a > 1 as a sum of fractions 1/b. a. Understand addition and subtraction of fractions as joining and separating parts referring to the same whole. b. Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model. Examples: 3/8 = 1/8 + 1/8 + 1/8 ; 3/8 = 1/8 + 2/8 ; 21/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8. c. Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction. d. Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.

5.NF.1 Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators. For example, 2/3 + 5/4 = 8/12 + 15/12 = 23/12 . (In general, a/b + c/d = (ad + bc) /bd.)
5.NF.2. Solve word problems involving addition and subtraction of fractions referring to the same whole, including cases of unlike denominators, e.g., by using visual fraction models or equations to represent the problem. Use benchmark fractions and number sense of fractions to estimate mentally and assess the reasonableness of answers. For example, recognize an incorrect result 2/5 + 1/2 = 3/7, by observing that 3/7 < 1/2 .

Quote of the Day: "If I had an hour to solve a problem, I'd spend the 55 minutes thinking about it and the last 5 minutes solving it." - Albert Einstein

Question of the Day (from students): Is it possible to have a mixed improper fraction?

Objective: Add and subtract fractions

Agenda:

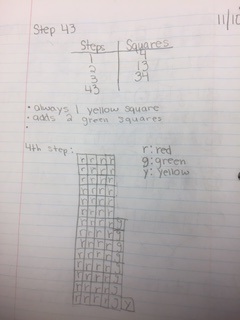
Visual Pattern #23
QSSQ
Review Homework (#6, #8, #11, #16). These problems either involved mixed improper fractions or whole numbers subtracted by a fraction
My favorite no 11 and 3/5 minus 6 and 4/5.
Notes on my favorite no
My favorite no 11 and 4/5 minus 6 and 3/4
Notes on my favorite no
Marker boards to practice other problems that forced students to find common denominators

Assessment: The marker boards was an effective assessment today. It is much quicker for me to assess if students are writing on marker boards because the writing is bigger. The students are also a tick more engaged.

The my favorite no problems were also assessed as every student showed me their index cards. Most of them tried to say that the first problem's solution was 5 and 1/5 even though 3/5 minus 4/5 is negative. They gave a thumbs up to notify me that they were able to recognize this mistake when we reviewed.

In the second MFN problem, students for the most part knew to get a common denominator. The most common mistake I saw was that they failed to change the numerator after the denominators were changed.

On the homework, I consistently saw students leave answers as 2 and 9/8 or when they were asked to subtract 1 and 2/7 from 2 they got 1 and 2/7 for a difference instead of 5/7.

Glass Half-Full: It was great to diagnose the mistakes and why they were mistakes today. Having said that, I'm on a personal day on Monday and have a long weekend with Veteran's Day before we meet again as a class. Old habits and ways of thinking have a hard time of dying quickly, so it will be interesting to see what students carry over from today until we meet again in five days.

The other great part of the class today was the connection between the quote of the day and the Visual Pattern. Students were unable to get the answer immediately in all of my classes, but some of them did eventually crack the code.

To keep this in perspective, this picture was taken from a student that two months ago would have a blank stare at a visual pattern problem. It is unbelievable to see some of the transformations in the problem solving processes with these students - even if they are not all solving the problems.

Regrets: We rushed reviewing the homework problems and I still believe most of the students who could not do 2 - 1 and 2/7 for homework still cannot do it now. This will undoubtedly be part of my lesson on Tuesday.

Link: I liked this Tweet from Mark Chubb who asks what is a better question. What is closer to one on a number 4/5 or 5/4? Or 4/5 is closer than 5/4 than 1. Show why using a number line.

Day 47: Fraction Introduction

Self Assessment checklist from the test
Review the Ratio Test
QSSQ
Fraction Notes
Hershey Bar
Adding and subtracting fractions with like denominators

Assessment: I tried to flip the classroom the day before this lesson by having students complete a Google Form after watching my video. About half of my students completed it.

Glass Half-Full: We defined the different types of fractions and what exactly a fraction is. Getting these core pieces is critical to making estimates and checking the work in future lessons with the four operations.

Regrets: This was a very easy lesson to create a pre-assessment for and I essentially did it with the Google Drive, but then I never bothered to differentiate the lesson. As the standards indicate above, this is a third grade skill. That being said 35% of students did not know how to convert between mixed and improper fractions, so it was worth the time to review for that crew, but the rest of the class could have been held to higher standards or given a harder task than the notes which they really already master.

Link: I follow Eric Sheninger on Twitter and I came across a nice Tweet from something he wrote back in August about a solution to negative people. Don't complain and if you do complain present two solutions to solve your problem or issue. He stole it from Jon Gordon's book No Complaining Rule. It's on my short list of must reads as I've also read The Energy Bus and Training Camp by the same author and gotten things out of those books.

Day 46 Ratios Test

6th Grade Math Standards: 6.RP.1 Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. For example, “The ratio of wings to beaks in the bird house at the zoo was 2:1, because for every 2 wings there was 1 beak.” “For every vote candidate A received, candidate C received nearly three votes.”
6.RP.2. Understand the concept of a unit rate a/b associated with a ratio a:b with b ≠ 0, and use rate language in the context of a ratio relationship. For example, “This recipe has a ratio of 3 cups of flour to 4 cups of sugar, so there is ¾ cup of flour for each cup of sugar.” “We paid $75 for 15 hamburgers, which is a rate of $5 per hamburger.” 29
6.RP.3. Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations. a. Make tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and plot the pairs of values on the coordinate plane. Use tables to compare ratios. b. Solve unit rate problems, including those involving unit pricing and constant speed. For example, if it took 7 hours to mow 4 lawns, then, at that rate, how many lawns could be mowed in 35 hours? At what rate were lawns being mowed? c. Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent. d. Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities

Objective: Write a ratio three ways in a word problem context; find equivalent ratios by getting a unit rate; solve problems with ratio reasoning; apply a tape diagram to solve for an equivalent ratio; apply a double number line to solve ratio problems; find the least common multiple; compare two different prices

Agenda:

Quote, Star Student, Question
Take the Test
Retake any previous assessments from this year
5, 4, 3, 2, 1 challenge (get to 20 through 30)
Read a book

Assessment: The test results were about what I would expect. This was a test that featured many concepts and covered almost all of the ratio common core standards, so there were definitely students with gaps. Class averages were in the high 70s. What will be interesting to see is how these gaps get filled moving forward. In general, ratios do not always correlate with future topics such as algebra and statistics, so I may explore getting these concepts in.

Here is an example of students getting two different answers (bottom is correct, top is incorrect) by doing the problem two different ways. I have used this problem for three years now and like the depth it forces students to use when they solve it multiple ways.

Glass Half-Full: On part three of the agenda, students were allowed to retake any test or quiz from earlier this year. Students have folders in my room which show me which questions that they have answered wrong on any prior test or quiz we have had at this point in the year. It's not always the most efficient way to differentiate (I would love to rely on software instead), but it does give students the opportunity to increase their grade and me the opportunity to reteach and motivate students to continue learning the skills that they lack. Students were retaking quizzes from September and October (not the exact questions, but similar ones) and answering them well. This was encouraging to me because I do not think there's anyway that these skills can be classified as simply memory activating their brains. They were truly capable of performing the skill and this is a sign of mastery.

Regrets: Many students approach me during a test to sneak an answer out of me. I very rarely will comply. I wonder what research says about providing assistance during tests. My personal view which was influenced by Rick Wormeli is that mastery is not mastery until it is independent.

Link: That quiz was a resource I just heard about on Twitter. Not very fancy, but seems easy to use and a good place for remediation, pre-assessment, and even homework.

Tuesday, November 8, 2016

Day 45: Ratios Study Guide

Which one doesn't belong (Number 11 from Mrs. Morgan)
QSSQ
Collect WQs and Review HW
Start the study guides
Review the study guides

Assessment: Circumventing the room as students worked on the study guide. The study guide is definitely longer than a full class. In the future I can cut problems out of the study guide. Most notably numbers five, six and any two of numbers fourteen through sixteen. It is a busy test with almost the entire ratio standard incorporated (with the exception of percentages using proportions).

Glass Half-Full: A colleague who teaches ELA came to observe my classroom last block and he was very complimentary of the way in which I have the students use highlighters to find the information that is important in a word problem. As he put it, treating word problems as close reading activities helps reinforce literacy skills and problem solving skills.

We also tried something spontaneous that the ELA teacher liked. All of the students were encouraged to send me a picture of them studying. The test was coming after a weekend and the study guide was given on a Friday. Experience has taught me that testing on a Monday inevitably leads to worse results. There are a number of factors that are likely to cause this - most notably that memory is not as strong so this was something worth a shot.

Regrets: Aside from what was already mentioned with eliminating problems, I feel as though students would also benefit from an answer key readily available to them on this study guide due to the high number of problems that they were asked to do. I also firmly believe students do not take advantage of this accommodation regularly because they are unaware of it and have never been taught with answer keys before. The security of knowing that they did the right process and got the right answer does not have to be exclusive to me walking around. Unfortunately we do not have Chromebooks on a 1:1 ratio (no pun intended given the content we were focused on) and I do not like to have to photocopy this many answer keys. I could have students check their phones, but my room gets awful service. Excuses are lovely but I can certainly navigate around all of these excuses.

Link: Warren Buffet drove people in a trolley to get out to vote. It was great to see the unified spirit of the country to just vote in so many instances (without actually following that with vote for ____). Having said that, Buffet of course did openly endorse Hilary.

Saturday, November 5, 2016

Day 44: Equivalent Ratios

6th Grade Math Standards: 6.RP.3 Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations. a. Make tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and plot the pairs of values on the coordinate plane. Use tables to compare ratios. b. Solve unit rate problems, including those involving unit pricing and constant speed. For example, if it took 7 hours to mow 4 lawns, then, at that rate, how many lawns could be mowed in 35 hours? At what rate were lawns being mowed? c. Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent. d. Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities.

Objective: Determine if two ratios are equivalent

Question of the Day: Would the points on a graph always be connected?

Agenda:

Estimation 180 Day 54 & Day 55
Quote, Star Students, Question of the Day
Review the homework or coordinate plane and ratios
Pepper
"One chocolate chip recipe makes 48 cookies and call for two cups of flour. A different recipe calls for 3 cups of flour and makes 60 cookies. Are these rates equivalent? Explain why or why not."
We looked at student answers to this question
Practice using the textbook on page 43 and 45.
Interleaving homework assignment started in partners

Assessment: There was actually a nice question in the textbook that asked students to determine if a rate per day and a rate per week was equivalent. About 90 percent of the class got it wrong, and quickly did the "ohhhh" when the students that got it right explained. I checked homework and the chocolate chip problem.

Glass Half-Full: I really enjoyed walking around the room during the problem that students did on the chocolate chip cookies. In the past, I have just given notes and showed students different methods. The methods were always either scaling or unit rate, but by letting students work they showed me ratio tables, double number lines, and least common multiple as alternatives to solving this problem.

Regrets: I do not think students fully grasp the concept of scaling yet and if they do they are not using the term scaling because I am leaving it out. I think this terms will be helpful to them in years to come. I also think this is the most frequently use way to compare ratios in the real world because it is the easiest. This is partially a flaw of the common core system. There are so many tools in the toolbox, but some tools are only necessary once in a blue moon while others require more wear and tear.

Link: 71 - 58 in the eyes of a second grade. When you listen to them it's a little better than when you look for how you want to do it.

Wednesday, November 2, 2016

Day 43: Graphing Ratios

6th Grade Math Standards: 6.RP.3 Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations. a. Make tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and plot the pairs of values on the coordinate plane. Use tables to compare ratios. b. Solve unit rate problems, including those involving unit pricing and constant speed. For example, if it took 7 hours to mow 4 lawns, then, at that rate, how many lawns could be mowed in 35 hours? At what rate were lawns being mowed?

6.NS.8 Solve real-world and mathematical problems by graphing points in all four quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate.

Objective: Graph ratios; list ratios into ordered pairs; describe the relationship in a graph of a ratio relationship

Question of the Day: Does it matter which unit goes on the top or bottom of a double number line?

Agenda:

Correct the mistake (see Double Number Line mistake described here)
QSSQ
Review the homework and pepper
Graphing review in partners as I passed back corrected weekly quizzes for students
Graphing kinesthetic exercise
Book Notes
Book Homework

Assessment:

Glass Half-Full: I really enjoyed my new touch to the kinesthetic exercise. We did so much vocabulary today that it was especially helpful. Coordinate plane, x-axis, y-axis, origin, ordered pair, independent variable, dependent variable, and linear function were all said for the first time today this year. That's a ton. The kinesthetic helped, but there's no doubt we will need to work on this some more.

Regrets: The book problems are always kind of lame, but they do not take near the effort it takes to re-create other problems that are more engaging and more relevant.

Day 42: Double Number Line & Ratio Tables

6th Grade Math Standards: 6.RP.3 Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations. a. Make tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and plot the pairs of values on the coordinate plane. Use tables to compare ratios. b. Solve unit rate problems, including those involving unit pricing and constant speed. For example, if it took 7 hours to mow 4 lawns, then, at that rate, how many lawns could be mowed in 35 hours? At what rate were lawns being mowed?

Objective: Apply a double number line to solve ratio problems; Create ratio tables to solve problems in which one ratio is given and only one of the other units is given; Use scaling to find equivalent ratios

Agenda:

Visual Pattern #18
QSSQ
Resuming the double number line gummy bears lesson
Double number line guided practice
My favorite no. If I mow 8 lawns in 14 hours, at that rate how many lawns could I mow in 49 hours?
Notes
Practice/Homework

Assessment: It was a busy day with a lot of content. I mostly circumvented to see how students were doing and gave light instruction at the board, but mostly let them try and fail. Here are a couple of the more common things I saw.

This first picture is from my favorite no. Only about 10 percent of students could do this, so most students required my instruction for how to find equivalent ratios. The student pictured here got much closer than most of the students. They demonstrated the ability to find a unit rate which would lead to an easy solution if they flipped it around to find hours per lawn.

Even during the notes, I was still trying to let them fail a little. Here the student continues to have a flawed definition of what a ratio is by leaving a difference of 10 between the two currencies. The analogy of if I had 10 Canadian dollars being worthless in American dollars goes over their heads so I try to use a wheels to bike analogy to explain away the error.

This last one is similar to the mistake above. I had students stand and repeat after me. Multiply to find equivalent ratios. Divide to find equivalent ratios. Don't add. Don't add. Don't add. Don't subtract. Don't subtract. Don't subtract. Unfortunately, the students and the co-teacher then bring out the argument that as long as your adding by two wheels on top and one bike on the bottom you can add (or subtract) just not by the same number. Their right. That's so much more complicated to think about though. Let's just call it multiplying.

Glass Half-Full: I had the students complete a Google Form for the homework. First time I've done it all year. It was great for the few students that completed My Favorite No correctly because they got to take a Chromebook and answer these questions in class instead of doing the notes.

Regrets: It was bad for the majority of students who completed the notes because they did not have time to use the Chromebooks in class and I never explained how to do the assignment. Oh well. There was so much going on in one day. Usually I split these lessons into two separate lessons, but with Election Day and Veteran's Day and assembly after assembly I did everything that everyone tells me not to do and rushed it.

Link: Socratic Seminar courtesy of a colleague who I got to see try this today in his 7th Grade ELA class. Always fun to try new things, but more fun when you don't have to be there.