Objective: Divide fractions in order to find a quotient; Place a fraction with a different denominators between two like fractions with numerators that are one apart on a number line (what fraction is between 11/3 and 12/3?)
Question of the Day: "Why is it that 3 and 4 will bring the same product and least common multiple, but 9 and 6 do not have the same product and least common multiple?"
Agenda:
- Determine what fraction is between 11/3 and 12/3
- Visual Pattern #32
- QSSQ
- Review Homework and Pepper
- Who Wants to Be a Millionaire (second class). All 13 questions are going to appear on the test (students do not know this)
Assessment: The students used individual marker boards during Who Wants to Be a Millionaire; I circumvented the room for homework and pepper
Glass Half-Full: The way the timing worked out in this lesson could not have been much better. The routine of steps one through four combined with the novelty of step five in the second class was the right balance for engagement and learning to happen across many types of learners. Everything done was assessable and gave students an indication of where they were proficient and where they were lacking skills (needed reteaching or simply to cross their T's).
Regrets: I could not do all 13 questions on Who Wants to Be a Millionaire as a result of reteaching as I found student misconceptions. Ultimately, I think I would have been better off if I had strategically placed a question with each operation as well as the objective of locating fractions between number lines back to back. What ended up happening was that one class never needed to find a fraction between two like fractions and another did nothing but find a fraction between two like fractions as a result of me trying to compensate for my mistake in the first lesson. Just need to find a balance between the two and could do so by skipping around on Who Wants to Be a Millionaire rather than doing each question one by one. Students these days do not really remember how Who Wants to Be a Millionaire is supposed to be played anyway.
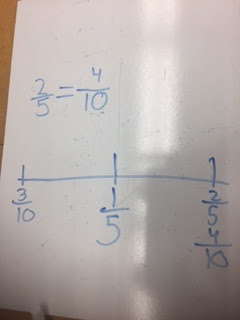
No comments:
Post a Comment