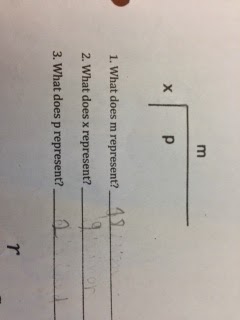Day 20: Prime Factorization

6th Grade Math Standards: 6.NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example express 36 + 8 as 4(9 + 2).
MA.4.a Apply number theory concepts, including prime factorization and relatively prime numbers, to the solutions of problems.
The Learning Objective: Factor a composite number down to all prime numbers

Quote of the Day: “ ‘There’s plenty of blame to go around!’ Really? Does there need to be? Can’t we just move on and solve the problem.” - John G. Miller from The Question Behind the Question

Agenda:

1. Jumpstart --> In one class we picked math partners for the first time and in the two others we did Connect Four since each class had not done this activity yet, but had done the other. 
2. We reviewed the homework. Students struggled with the idea that 121 was a composite number initially (this was a big deal the day before for me that they really think before declaring a prime).
3. We took notes on prime factorization
4. Students did a problem independently using the "birthday cake method" (see picture below)
5. As students entered class for a second time I did another formative assessment using the number 13 as a factor because I was confident they would struggle when I stepped away from the 2, 3, 5 prime number comfort zone.
6. Students worked with a math partner on the homework. I told one class to start with word problems thinking they would want to struggle with the challenges with me in the room rather than doing it at home.

The Assessment: I'd like to think there were four today. First of all, almost every morning as students get to their lockers I'm holding up a marker board with a basic problem from the day before. Today I asked is 91 was prime or composite. One out of nineteen students said that it was composite - and that student couldn't tell me what factors produced 91 other then 1 and 91. Obviously this is a tough problem to do mentally, but that so many students would instantly conclude that 91 was prime concerned me. As I told each one that they were wrong, I sensed a greater degree of caution in class on numbers such as 1001 (7 x 11 x 13).

The second assessment was me looking at their homework. Students clearly know the definition of prime and composite. Every student correctly identified even numbers as composite. That said, they are still struggling with numbers that are divisible by 3. Number like 129 and 57 were tripping them up. Also the aforementioned 121 was difficult, but it was nice to see so many students perk up when I declared the numbers were composite and they saw what number caused this.

The third assessment was a bit more of a cupcake. I had them factor either 210 or 105 as a fourth example in their class notes. They passed this with flying colors.

The last assessment was the students entering the room doing the problem featured in the picture above and also below. It's always painful to see a student understand the process, but simply miss one step in the calculation process. The student even started to do it out, but then erased it  (see the top right of the picture in lighter looking pencil) thinking that 2 went into 78 only 34 times.

Homework: Tonight I had the students practice 8 numbers including the difficult 1001 to find prime factors for. I also asked theory questions such as why 2 is only the even prime number and if someone's lock combination involved a prime factor of 435 what could the combination number possibly be?

My Glass Half-Full Take: I didn't even mention that I was circumventing the room for about twenty-five minutes as they started the homework. I feel confident in my assessments that the students understand how to get the prime factors of a number.

One Thing to Do Differently: In a month, if I give the directions "write 96 as a product of prime numbers" I still feel like the class will have difficulty. If I gave the directions "make 96 a birthday cake" or "make 96 a factor tree" they will pass the test with flying colors. Thus, I'm going to ask them in a month "write 96 as a product of prime numbers." And if they don't get it, we'll see it again two weeks thereafter.

Link of the Day: In the theme of prime and composite, why one is the loneliest number.

Day 19: Prime and Composite Numbers

6th Grade Math Standards: 6.NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example express 36 + 8 as 4(9 + 2).
MA.4.a Apply number theory concepts, including prime factorization and relatively prime numbers, to the solutions of problems.

MP.1 Make sense of problems and persevere in solving them. 

MP.5 Use appropriate tools strategically.
The Learning Objective: Differentiate between prime and composite numbers

Quote of the Day: "Americans spend twice as much time on Facebook as they do exercising. And the younger the age, the worse the effects. The average college student spends three hours a day checking social sites. According to a USA Today report, the grade point average of college students who regularly use Facebook is a full point lower than their peers who do not...American workers are interrupted once every 10.5 minutes by things like emails, texts, or tweets. Once interrupted, it takes an average of 23 minutes for them to get back on task.” - Rick Pitino

Agenda:

1. Self-Assessment from Friday's Quiz
2. Journal about the quiz
3. Create line graph from the three quizzes so far this year
4. Review the quiz as a whole class
5. Notes on prime and composite numbers
6. Prime numbers challenge - what day of the year was yesterday (September 28th)? Is that day a prime number? How can you tell?
7. Start the prime number homework and include a challenge.

The Assessment: My primary assessment to see where students stood against the objective was for students to classify the numbers 10, 25, and 29 as either prime or composite. I circumvented the room and they passed with flying colors.

That said, their minds were not pushed in the same way as they were when I asked what day of the year September 28th was. I rephrased this question several ways. How many days has it been since January 1st? How many days have there been in 2014? How many days in the calendar year have we had so far? Eventually they understood the question, but arriving at the answer was not even close to as easy as I would have imagined. I learned what months had thirty days when I was in second grade. And I'm pretty confident in saying that my classmates in second grade mastered this at the stage in their lives as well. I'm not saying that these kids aren't learning anything in lower grades either - in fact I feel the opposite. They are learning more and more sooner than I was at their age, but perhaps that's a problem. Finland's school days are shorter and their standards are fewer, but yet their mathematical achievements are much higher? Perhaps less is more. Perhaps the phrase "Thirty days have September, April, June, and November" is more important than estimating lengths to the nearest meter (both of these are second grade standards in Massachusetts but only the lengths to the nearest meter is a national common core standard).

In any case, it was fun as a teacher when I would go to the board after they struggled for a few minutes and they begged me not to tell them how many days there were. They worked in partners and continued to struggle. Eventually a couple students did get the answer. I was pleasantly surprised that using tools (yes the calendar above is a tool) came up in the lesson today. 

All that being said the answer of 271 was my main reason for bringing this whole question up. I wanted the students to explain if 271 was prime or composite. By the time I asked them this question they were either spent from working out the previous problem or had no motivation to solve this one. They all guessed a simple yes or no. Nobody bothered to divide by seven until I commanded it. Nobody touched whether or not 11 or 13 or 17 went in. And this begs the question, did the students meet the objective? 

Homework: This worksheet as well as our 2nd Weekly Quiz. The homework was deceptively difficult or as I would tell the students "filled with wolves." Students had the most difficulty with numbers like 121 and 57 because they are not divisible by the numbers with "easy rules."

My Glass Half-Full Take: It only takes one student. Today a student stayed after school that had not all year to complete a weekly quiz, homework, and help learn from mistakes made on the quiz from last week. The day was an overall struggle. Students did not know how to fill out the graph of their math quizzes, our self-assessment form is due to the administration team later this week, and I'm awaiting transcripts for credits from this summer and last summer after schools never notified me that my grades were in. I was in a bit of a funk from the first block on and every little obstacle I faced seemed much worse than it really was because of my mindset (so much for Day 18's quote of the day!). In any case it was good to have something positive come from the day at the very end of the day.

One Thing to Do Differently: In what I would deem a bad day for me, it's hard to pin this to one thing. Perhaps from the get go I should have put the students' quiz scores as a percentage (what they are used to) as opposed to leaving it as a fraction. They do not know how to convert from fractions to decimals yet. My partial goal in leaving these grades as a fraction of course is that they can learn this valuable skill and they see its use. My other goal is that they look not at the score of the quiz but turn to the parts they answered incorrectly or did not have the knowledge to answer at all.

That said, the amount of time it took for students to graph their results, look back at a quiz we took last week and graph that, and also just to do the journal entry about what went right and wrong with this quiz took long enough. I ended up spending 50 of our 100 minutes together today going over the quiz and the paperwork associated with the quiz (more time allocated to the ladder than the former). It was frustrating for me to waste this time that could have been spent on assessment of the objective, and obviously I did not deal with it well. Tomorrow I'm going to forget about it though and start fresh. There is still value in getting students to write how they can improve their study habits and in seeing what simple mistakes students were making to correct that in the future.

Link of the Day: I learned as much as they did.

Day 18: Least Common Multiple, Greatest Factor Test

6th Grade Math Standards: 6.NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example express 36 + 8 as 4(9 + 2).
MA.4.a Apply number theory concepts, including prime factorization and relatively prime numbers, to the solutions of problems.

The Learning Objective: Find the least common multiple of two or more numbers, find the greatest common factor of two or more numbers, apply the rules of divisibility for 2, 3, 4, 5, 6, 9, and 10, and define the rules of divisibility for 2, 3, 4, 5, 6, 9, and 10

Quote of the Day: "Anytime I find myself drifting into a negative mindset - and this happens to everyone - I realize that I'm on the road to failure. And more often than not, the way out of that mindset is to get back to work." - Rick Pitino

Agenda:

1. Take the quiz
2. Start the weekly quiz
3. Explain our homework which is to go online and sign in to the online textbook then answer a question using Google Forms to prove that the student got on the online textbook.
4. Clean out the binder
5. Connect Four (not the Connect Four you think)

The Assessment: The quiz, Connect Four

Homework: Use the online text then answer this question.

My Glass Half-Full Take: We had a fire drill today and it went very well. At the beginning of the year I told all of the students that emergencies and how we prepare for them are the most important thing that we can do in a school day. I brought up the example of Newtown, Connecticut on that first day of school although we didn't discuss it in great detail, but just to drive how the point of how potentially dangerous and serious a situation could be. It is easy for the students to respond the way that they should right after I give that speech but that was seventeen school days ago. Today it appeared they got the message. Everyone knew where to go and understood once we got outside to listen for me to call off the attendance.

One Thing to Do Differently: I only got to Connect Four in one out of three classes and I find this assignment to be excellent on a number of different levels. It gets students out of their seats, gets students to be social, is a formative assessment, and involves the type of collaboration that I'm pretty certain will contain a math focus. It could have been useful to do this a day earlier in the last five minutes of class.

Link of the Day: I liked this game for teaching place value of decimals, comparing decimals, and getting students to think strategically about decimals. Way more engaging than having them memorize place values.

Day 17 Review for Test on Multiples, Factors, and Divisibility

6th Grade Math Standards: 6.NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example express 36 + 8 as 4(9 + 2).
MA.4.a Apply number theory concepts, including prime factorization and relatively prime numbers, to the solutions of problems.

The Learning Objective: Find the least common multiple of two or more numbers, find the greatest common factor of two or more numbers, apply the rules of divisibility for 2, 3, 4, 5, 6, 9, and 10, and define the rules of divisibility for 2, 3, 4, 5, 6, 9, and 10

Quote of the Day: "I read about two hundred executives who were asked what makes people successful. The number one quality they cited was enthusiasm, not talent - 80 percent of them recognized that there needed to be a fire within to achieve success." - John Maxwell

Agenda:

1. Jumpstart with least common multiple questions as I checked the homework
2. We reviewed two word problems from the homework on the board. 
3. The students worked with a partner on this review sheet.
4. In the second part of class, the students worked with a different partner on another review sheet. I thought it was critical that they had a different partner to increase the diversity of ways to solve problems. I circumvented the classroom to see how students were doing. 

The Assessment: Checking the homework and also circumventing the classroom as the partners worked.

Homework: The weekly take home quiz is due in the next class and we are also taking a test on the above learning objectives.

My Glass Half-Full Take: Not pictured anywhere in the agenda I had students come to my class after school and work on a problem that we are going to see in two weeks about cookies and muffins. The gist of the problem is that a bakery is giving away a muffin to every 6th customer that comes in and a cookie to every 4th. The problem was a released MCAS question I believe.

The way we worked on the problem was through acting it out. I brought in my nieces toy cash register and purchased the cookies and muffins from a local bakery. The kids really enjoyed it. I am looking forward to showing it in a couple of weeks and hope that it will lead to increased understanding of what the problem is asking.

One Thing to Do Differently: After the students took the quiz it is apparent that least common multiple word problems are an issue. Students were adding the multiples of 3 and 4 to get an answer of 7 at an alarming rate. That is precisely why we as a sixth grade math team have the weekly quiz. The cookies and muffins will serve their purpose.

Link of the Day: I found this blog on Twitter with a search of decimals and #mathchat. It's called Math Minds and it comes from an elementary math teacher. I really enjoyed the diversity in the reasons that students gave for how they arrived at a solution.

Day 16: Least Common Multiple Day 2

6th Grade Math Standards: 6.NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example express 36 + 8 as 4(9 + 2).
MA.4.a Apply number theory concepts, including prime factorization and relatively prime numbers, to the solutions of problems.

The Learning Objective: Find the least common multiple of two or more numbers.

Quote of the Day: "Don't worry about whether you're better than somebody else, but never cease trying to be the best you can become. You have control over that; the other you don't. Time spent comparing yourself to others is time wasted." - John Wooden

Agenda:

1. Jumpstart - Mystery Number 
   
2. Review the homework & discovering the least common multiple shortcut
3. Least common multiple of 8 and 12 (formative assessment on an index card)
4. The clickers to decide if a question was asking for greatest common factor or least common multiple
5. Start the least common multiple homework
6. Work with math partners on the rest of the LCM homework

The Assessment: Finding the least common multiple of 8 and 12, utilizing the clickers, checking the current homework (due tomorrow) and the past homework (due today).

 Most students prefer the option below, and I prefer the option above (it demonstrates more mathematical fluency and can be used to tackle much harder cases such as the least common multiple of 22 and 36). In any case, I accept either way as they lead to the same outcome.

Homework: Word problems that include finding common multiples and the least common multiple.

My Glass Half-Full Take: I am seeing evidence in my assessments that students are able to find a least common multiple. In one class, only one student was finding the greatest common factor of 12 and that student recognized the mistake shortly thereafter.

One Thing to Do Differently: I think coming up with a line of questioning ahead of time for the discovering the least common multiple shortcut activity would allow it to go better. Some questions to include are these:

• What do you notice about finding the solution to the least common multiple of...
• 3 and 4
• 2 and 5
• 5 and 9

•  What do you notice about finding the solution to the least common multiple of...
• 10 and 15
• 6 and 8
• 8 and 12

•  If they do not see the pattern after a couple minutes, ask them to find the greatest common factor between the numbers first or even ask if the numbers are prime and composite (which isn't entirely the pattern but one class saw this first and was able to make the connection soon thereafter). 

Link of the Day: Every year after the state testing, I spend some time doing financial lessons with the students. I don't understand why there isn't a financial literacy piece in the standards (even though President Obama has acknowledged financial illiteracy is an issue by signing Executive Order 13530, but anyway the standards are the standards), but this lesson from Yummy Math tackles standards and literacy in my opinion.

Day 15: Least Common Multiple

6th Grade Math Standards: 6.NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example express 36 + 8 as 4(9 + 2).
MA.4.a Apply number theory concepts, including prime factorization and relatively prime numbers, to the solutions of problems.
The Learning Objective: Find the least common multiple of two or more numbers.

Quote of the Day: “You can take the best team and the worst team and line them up and you would find very little physical difference. You would find an emotional difference. The winning team has a dedication. It will have a core group of veteran players who set the standards. They will not accept defeat.” - Merlin Olsen, Los Angeles Rams

Agenda:

1. Estimation 180 the smaller stapler
2. Review the homework --> this wasn't great as many students did the first 8 problems in class and then didn't follow up with the 9th problem at home. 
3. Free write regarding how students would handle 8 hot dogs in a package and 12 hot dog buns in a package.
4. A look at how George Banks from Father of the Bride handled the same situation. 
5. Least Common Multiple notes (two word problems)
6. Start the least common multiple homework (I did one, they showed me one, then they were off and running).
7. Form Math Partners for quick grouping (done today because classes are pretty much final in school now)
8. Utilize the TurningPoint clickers to assess six different questions:

• Is 18 a multiple or factor of 9?
• Is 3 a multiple or factor of 9?
• How many multiples does the number 9 have?
• How many factors does the number 9 have?
• What is the greatest common factor of 8 and 10?
• What is the least common multiple of 8 and 10?

After the assessment it was pretty clear that we had some work to do in differentiating what a factor and multiple were.

The Assessment: Turning Point, a fist of five after the two notes problems, the free write exercise, the previous night's homework, the students that passed in their weekly quiz today to be highlighted for potential wrong answers, and the opportunity to start homework in class.

Homework: The students had 16 different least common multiple practice problems (the last five were more challenging as they involved more multiples), the weekly quiz is due in three more days, and we have a quiz on Friday to start studying for.

My Glass Half-Full Take: These are why I teach. Funny. Thoughtful. Creative. Analytical.

One Thing to Do Differently: The homework worksheet has it's boring parts. There are zero word problems. The students are doing the typical drill and kill. Once they get one right, the process of finding the least common multiple is clear. I could have done two things to change the pace on this. The first is sprinkle in a change of directions and give them some greatest common factor problems as well. The second would be to ask if there was an alternative way to find the answers other then simply listing the multiple (which is the only way I showed them). The least common multiple of 3 and 4 is 12, which is simple to arrive at when students see all that needs to be done is simply multiply the two numbers. When 10 and 6 are used instead and they see the answer is actually lower than 60 though it blows that whole theory up.

Link of the Day: Not all of these are great for teaching kids, but the site I pulled the Father of the Bride clip from today is from Harvard and it is called Math in the Movies.

Day 14: Greatest Common Factor Hands On

6th Grade Math Standards: 6.NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example express 36 + 8 as 4(9 + 2).
MA.4.a Apply number theory concepts, including prime factorization and relatively prime numbers, to the solutions of problems.
The Learning Objective: Find the greatest common factor of two or more numbers.

Quote of the Day: "Walt Disney's request for a bank loan was denied 301 times before he finally got a yes." - John Maxwell

Agenda:

1. Jumpstart with three Greatest Common Factor problems
2. Review the jumpstart and homework
3. Find the greatest common factor in my group of tickets and cards.
4. Begin the homework
5. Visual Patterns 3 and 4 (if the homework is completed). 

The Assessment: I partnered students up and gave them either a stack of tickets or trading cards that could be sorted into two groups. Once the cards and tickets were sorted, I asked students to divide them into as many groups as possible so that each type of card or ticket was included the same amount of times in each group. It sounds confusing because it is. Here's a better look at what the students did once the task of counting how many of each card was taken care of.

Looking at the top picture of Michael Jordan and Shaquille O'neal you can see that there are 10 Shaq cards and 5 MJ cards, so the cards were broken up into groups of 2 Shaq cards and 1 MJ card. The kids really enjoyed the activity and also were fascinated with the collection that I have acquired (nobody took the free opportunity to make a crack about how old I must be - very polite crew). All that being said, they could do this in a hands on activity but struggled more in the word problem version of this same problem. Here's the problem that they got in the homework:

Barbara is making candy bags for her birthday party. She has 24 lollipops, 12 candy bars, and 42 pieces of gum. She wants each bag to have the same number of each kind of candy. What is the greatest number of bags she can make if all the candy is used? How many pieces of each kind of candy will be in each bag? 

I'm thinking that the problem from the homework is very boring and wordy. Whereas my example students got to play and didn't have to read. It was more engaging and less intimidating. It's tricky though because our friend Barbara is precisely how the students will be assessed while I feel like the basketball cards is a closer representation to a real world problem.

Homework: The students were given almost a full class period to do the homework which was nine greatest common factor questions (with varying levels of Bloom Taxonomy).

My Glass Half-Full Take: I had students stay with me during lunch for the first time this year to work on divisibility rules and I felt like a lot got accomplished. I also had a few students stay after school, and again I believe a good deal was accomplished. This time is crucial for students to get extra help and for me as their teacher to reach them when they are struggling in the bigger fish tank of the classroom.

One Thing to Do Differently: In my third class of the day, I did a problem similar to the Barbara problem with the class after we used the trading cards and tickets. I drew pictures to help the class see it better. I would do that with all three classes if I need to teach this lesson again next school year. It's a good way to connect the hands on and the hands off.

Link of the Day: If we want innovation, we need diversity. Of course diversity also leads to a decrease in trust, lower communication and other downsides according to this same article.

Day 13: Greatest Common Factor

6th Grade Math Standards: 6.NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example express 36 + 8 as 4(9 + 2).
MA.4.a Apply number theory concepts, including prime factorization and relatively prime numbers, to the solutions of problems.
The Learning Objective: Find the greatest common factor of two or more numbers.

Quote of the Day: "Do the right thing, day after day. There are no shortcuts to anything worthwhile." - John Maxwell

Agenda:

1. Estimation 180 Day 16 and Day 17
2. Greatest Common Factor Notes
3. Divisibility Rules written in the journal
4. Start the Greatest Common Factor homework

The Assessment: After my first class today I had a prep. While walking to the office one of the three other math teachers mentioned to me that she was telling all the students to write the divisibility rules in their journal and if they didn't know them, she was going to make them stay after school Monday to practice. I liked the idea. Sure, divisibility rules is rote learning, but I'm such a big believer in fluency as a ticket to higher thinking. I also thought it was fair given that I have written on the board since Monday (four straight nights) that the students should study their divisibility rules.

I did three more assessments during class. As part of the notes, I had students complete two problems independently. They stood up when they were done. The other greatest common factor assessment was on the homework. In two out of the three classes I had time to go around and check off the first problem. Finally, I returned students' weekly quizzes with highlights of wrong problems for them to fix.

Homework: Greatest Common Factor worksheet

My Glass Half-Full Take: Friday was a great class. The estimation activity once again proved why staples can be so fascinating. The notes were excellent in repeating points of emphasis (list factors in pairs, always start with one and the factor itself, and take advantage of divisibility rules). And the assessments accomplished what they should. The students know where they stand, I know where they stand, and we have a plan to fix what should be fixed.

As an aside I was reading from a piece of literature I got from a college basketball coach in which he advocated there is no way of showing you care quite like a hand-written note - especially in light of the technology in our world today. I thought of six examples to date where I was proud of student effort, enthusiasm, or intentions to this point of the year and just now wrote each of them letters. I'm excited to give them out tomorrow and look forward to continue to use this as a tactic in strengthening student habits and my relationship with the student.

One Thing to Do Differently: We had a problem in the notes that asked the students to find the greatest common factor of 28, 56, and 84. I think in the future I would like to add a piece into the notes that asks students to predict what the greatest common factor will be before doing the work. None of the students in the one class I did this with correctly predicted the greatest common factor, so this is a great tool to influence students that they need to show the work.

Link of the Day: On my way to New York City this weekend, I heard a Ted Talk by Rita Pearson for a second time. Her voice was made for speaking. According to the podcast, Rita recently passed away, but much like her mother her legacy continues. This video on the necessity for relationships has well over half a million views on YouTube.

Day 12: Multiples

6th Grade Math Standards: 6.NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example express 36 + 8 as 4(9 + 2).
MA.4.a Apply number theory concepts, including prime factorization and relatively prime numbers, to the solutions of problems.

The Learning Objective: List the multiples of a given number.

Quote of the Day: "Don’t tell me how tough the situation is; show me how tough you are facing the situation.” - Jay Bilas

Agenda:

1. Weekly Quiz Jumpstart
2. Multiples My Favorite No
3. Multiples Notes
4. 5 Minutes of ?'s - I split the case into a waive of 2 minutes, 2 minutes, and 1 minute. Six to seven students answered questions in each waive. The questions were mostly vocabulary oriented.
5. The Multiples Contest - The other math class and my class went back and forth saying multiples to one another until they sounded shaky. 
6. Multiple vs. Factor Formative Assessment 
7. Marvelous Multiples Designs
8. The Sieve of Eratosthenes
9. Multiples HW

 







The Assessment: The My Favorite No Today asked students to list four multiples of 12. When I collected the students' work, more than half of them listed factors instead of multiples. This was exactly what I expected. At the end of this first class, I played a game I called five minutes of questions. Among the questions I asked the students were: What are the multiples of 4? What are the factors of 4?
In the second part of class, I asked that students list at least two factors of 12 and two multiples of 12. Only three students could not do this task at that point. I did this instead of asking them to list all factors because that would be an obvious give away between the differences in a factor and multiple. Afterwards I mentioned that they could list multiples forever. 



Homework: The students continue to work on their weekly quiz, but the assignment that is due tomorrow is the Multiples Homework

We input the divisibility rules as part of this homework. It was done ahead of time, but in my opinion this is still a skill that students have not mastered and a very good idea for this assignment.

My Glass Half-Full Take: In six years I have never had more confidence that students are able to differentiate between what a factor and multiple are.

One Thing to Do Differently: I think the Sieve of Eratosthenes is an excellent learning experience, but I definitely rushed it and tried to squeeze it in today. The objective of the lesson is to "discover" the prime numbers. Students start by crossing out one, circling two, and then coloring all multiples of 2 from 1 to 100. The Math Forum gives more details here.

I think I would have rather rushed the "Marvelous Multiples" activity and had the students on a clock of spending no more than ten minutes on that activity. The problem was that myself and the co-teachers were passing out tape, staples, etc. I should have put more students to work to make the process more efficient.

Link of the Day: The power of whiteboards and whiteboard space. I can work on this.

Day 11: The Weekly Quiz Party

6th Grade Math Standards: 6.NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example express 36 + 8 as 4(9 + 2).
MA.4.a Apply number theory concepts, including prime factorization and relatively prime numbers, to the solutions of problems.

The Learning Objective: Find the factors of numbers from 1 to 100.

Quote of the Day: Today was a half day so I did not bother to do a quote with 20 minute classes.

Agenda:

1. I checked homework as students read over the permission slip that was sent home for the weekly quiz.
2. We reviewed the factors homework. 
3. I went over the expectations for the weekly quiz with the class.
4. The students learned about how they can "Dominate" the weekly quiz. 
5. The students had the opportunity to start the weekly quiz in class. 

The Assessment: I checked the homework and noticed that many students left the number itself out of the list of factors. I also noticed that students were not including 7 and 14 as factors of 98 since we never discussed a divisibility rule for 7.

Homework: Students are going to turn in their weekly quiz tomorrow for a 5 point bonus.

My Glass Half-Full Take: This was the third straight year that our sixth grade math teachers have utilized a half-day to celebrate the first weekly quiz. The weekly quiz is for me the single greatest assessment that we can do in mathematics. Here's how it works:

• Every question is review.
• It is a take home quiz, but if the students are responsible they can see teachers after school for help. I tell them I don't mind if they get help from someone at home either (I trust that people at home want their child to learn just like I do). 
• As the year gets rolling, we will typically spiral back questions that students struggled with the month before. If they struggle on this again on a weekly quiz we continue to pound that topic on the weekly quiz. We make it so that some standards just can't hide. 
• It is a monster when it comes to making corrections. The teachers correct them daily to give the students an opportunity to fix their mistakes before they are truly due on Friday. 

The hardest part is of course getting the students to buy in. That's what today is for. Here's what we do to motivate the students:

• Weekly quizzes are worth 20% of their grade.
• For students that download it online a week in advance and turn the whole assignment in on Monday, we give a 5 point bonus. 
• There is a 100 Club for students once they receive five perfect scores. They also design a card that hangs from our ceiling that we call "The Hall of Fame."
• We have inter-team and inter-teacher competitions for who can get the most 100s. 
• We recognize all students that do the assignment the first opportunity they have with a "Grit Board" in the back of the room.  
• Today we had seven teachers wearing "light up a dark room orange" shirts that said WQ on the front and "When is it due?" on the back. I even wore orange pants and an orange top hat (I was Lloyd Christmas for Halloween once upon a time). 

Before it's all said and done it is an exhausting undertaking, but the goal is student learning and in my five years I don't think any assessment does it better.

One Thing to Do Differently: I wish I put out a video on the topic of Multiples ahead of time in caes students wanted to sneak a peak at the topic.

Link of the Day: Dan Meyer says we need to focus more on student question development if we want students to be engaged in what they are learning - not simply including problems from the real world. Oddly enough he writes about this the day after my cell phone problem.

Cell Phone Dilemma

I was doing the math for deciding what to do with my cell phone plan and had to write down what the problem is. I've been using more data than ever before this month because I have ditched the radio for podcasts on the ride into work. That prompted this in an email from Sprint:

As of 09/15/2014 at 12:57am, you have used 952554.00 KBytes of your 1048576.00 KBytes monthly Sprint 3G/4G Data allotment while on the Sprint network. If you exceed your monthly usage cap, you will incur overage charges of $0.014 per MB until your usage is reset on 09/27/2014

I looked up my options. I could add unlimited Data for $20 and Sprint would also give me annual upgrades (which I could care less about so let's just throw that out and concentrate on $20 for the unlimited data). They also offered 3 GB for $5.00. And of course the third option is I could also just let things ride and pay the $0.014 per MB.

I think that's all the information you need to make it somewhat interesting, but in order to truly get the most out of this problem it helps to know the date that the usage will be reset. That date is September 27th.

A couple hints: Breaking it down, I had to look up the ratio of KB:MB:GB. I also had to determine at the rate that I was using data what my expected amount of data would be from now until September 27th. I also wanted to see how much data I could use without going over if I changed nothing. This was a great lesson for sixth graders in terms of 6.NS.3, 6.RP.1, 6.RP.3, MP1, MP2, MP4, MP5, and MP6. I believe if I did this as a lesson I would give the students a calculator because the reasoning is high enough from the vantage point of a sixth grader.

Day 10: Writing All the Factors

6th Grade Math Standards: 6.NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example express 36 + 8 as 4(9 + 2).
MA.4.a Apply number theory concepts, including prime factorization and relatively prime numbers, to the solutions of problems.

The Learning Objective: Find the factors of the numbers from 1 to 100.

Quote of the Day: "You can't get much done in life if you only work on the days that you feel good." - Jerry West

Agenda:

1. Jumpstart that asks students for the divisibility rules for 2, 3, 4, 5, 6, 9, and 10. It also asks students to define factor, composite number, and prime number
2. Review the divisibility homework
3. Pepper (ask about vocab terms and examples of vocab terms)
4. Notes on factors. I just defined factor again and had students try four examples.
5. The students put together factors of 10, 12, 16, 20, 24, 36, 48 and 57 to be hung from the ceiling (after we do the same thing for multiples in two days). We called this "Fabulous Factors."
6. The Factor Game
7. Factor Homework explained to students

The Assessment: At the start of class, I checked all students homework for application of the divisibility rules and also asked students to write the rules without looking at their notes. I collected their work.

We played Pepper so that all students could show me they knew or didn't know the vocabulary. We practiced until they got five questions correct in a row.

In addition, students put together the "Fabulous Factors" independently.

Homework: This factor worksheet and I also told students to continue to practice their divisibility rules because they did not memorize them in many cases last night.

My Glass Half-Full Take: We spent around 70 minutes talking about factors all told today.

One Thing to Do Differently: I would have liked to have done a Pepper contest with my three different classes to see which class could get the longest streak of consecutive questions. I like these types of competitions because it promotes class camaraderie and teamwork.

Link of the Day: Microsoft acquired Mojang the maker of Minecraft. I wonder if there's a way for me to assess students on Minecraft with my standards. Should I start playing? It seems like a pretty big commitment of my energy.

Day Nine: The Divisibility Rules

6th Grade Math Standards: 6.NS.2 Fluently divide multi-digit numbers using the standard algorithm.
6.NS.4 Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example express 36 + 8 as 4(9 + 2).
MA.4.a Apply number theory concepts, including prime factorization and relatively prime numbers, to the solutions of problems.

The Learning Objective: Use the divisibility rules.

Quote of the Day: "Humility is the quality essential to sustained success, and a lack of it is the major stumbling block for those who find success for a time, then lose it...arrogant people spread around their failure with blame. When things go wrong they lash out and blame others." - Rick Pitino

Agenda:

1. Quiz Self-Assessment
2. Journal on what went well, the simple mistakes, and the concepts that still are not understood from the quiz
3. Divisibility Notes
4. Divisibility Independent Practice
5. Divisibility Flashcards
6. Divisibility Song
7. Divisibility Homework

The Assessment: The independent practice. I gave the students the numbers 360, 43, and 2,700 to try to see if 2, 3, 4, 5, 6, 9 and 10 went in using the rules of divisibility.

Homework: Divisibility Practice worksheet.

My Glass Half-Full Take: I was half listening to TED Talk radio on the way home today and there was one topic that struck me. Someone who went on to win a Noble Prize got their start in whatever it was they were doing by asking their father why a ball always gravitated to the same spot in a wagon when he was young. The father said it was inertia. When the child asked what that was, the father simple fired back that it was a scientific reason for why the ball always ended up in the same spot of the wagon. The child was curious and the rest is history.

Today the students were not the least bit curious about divisibility rules. I left school a little dejected with that typical feeling of "Why don't my students want to learn?" And then I realized that I never hooked them. I never sold what I was teaching ahead of time. I'm not sure if I need to add a category to this blog called the hook, but tomorrow I will hook them.

One Thing to Do Differently: Besides the hook, I distributed flashcards in every class. I wish that I had cut the flashcards ahead of time. For some students this took way too long. I also wish that there was time built in for the students to practice with each other, but then again it would have been hard to take something out.

Link of the Day: Pretty cool post from Anne Joseph of the Huffington Post on 35 Secrets of Brilliant Coaches. I love the idea of not trying to break bad habits (it's really really hard), but instead trying to build new ones.

Day Eight: Operations Quiz

6th Grade Math Standards: 6.NS.2 Fluently divide multi-digit numbers using the standard algorithm.

I also tried MP8 Look for and express regularity in repeated reasoning, but the students did not see the regularity until I pointed it out to them. 

The Learning Objective: Apply the correct operation to solve a word problem, define product, factor, sum, difference, and quotient, identify the three parts of a division problem (divisor, dividend and quotient), calculate using the four major operations in one step problems

Quote of the Day: "Never lie; never cheat; never steal. Don't whine; don't complain; don't make excuses." - John Wooden on his father's rules of three

Agenda:

The Assessment: The quiz.

Homework: In two of the classes, students were able to use the netbooks and try Get to 10 as well as 2048. I listed both links online and asked students to try out both. I really like Get to 10 as it is an engaging way to practice basic facts without making it seem like a chore. I do wish they would add parenthesis to the basic features.

My Glass Half-Full Take: I'm glad that I showed the students the game 2048. I just found out about it earlier in the week, and it was a quick turnaround time for me to introduce something that was new to me. Often times I forget about things like this and never introduce them. Turns out several students were already well aware of this app.

One Thing to Do Differently: I don't know if I would do this worksheet differently or not. The students saw this worksheet and completed all fifteen problems by showing the work using the standard way of calculating a two or three digit multiplication problem. It was the first thing students did when they completed the quiz and almost every student completed this sheet. Not one student noticed the pattern of one factor going up while one factor goes down. Not one student noticed that their products were decreasing from the problem before in a pattern. What I could have done differently was ask students to look for a pattern in the directions, but I'd rather instill in them that it is their job to always look for a pattern. What I did for one class was tell them to complete the problems in order, but I think they saw this as just me explaining another beginning of the year routine or something, and not as a hint.

Link of the Day: This article came from the New York Times. Students are generally more interested when they are working with someone on something (either together or in competition). Students are also more likely to learn when they see the relevance of something. This might seem obvious, but the last point in particular is thought provoking. Perhaps students journaling about why a standard or topic is relevant on occasion will help increase motivation, perseverance, etc.

Day Seven: Operations Study Guide

6th Grade Math Standards: 6.NS.2 Fluently divide multi-digit numbers using the standard algorithm.

The Learning Objective: Divide in order to find a quotient; check the calculation to verify an answer

Quote of the Day: "Discipline yourself and others won't have to." - John Wooden

Agenda:

1. Jumpstart on division exclusion or the ticket to leave (depending on the class)
2. Review the division homework
3. Ticket to leave review
4. Begin the study guide

End of Class 1

1. Finish the study guide
2. Journal on how to study and check work
3. Do three division word problems as part of our homework 
4. Visual patterns 1 and 2

The Assessment: I checked all students homework. I also went back and looked at students that made mistakes from the third day of school on subtraction and had five of these students do a borrowing problem that included a zero with precision. I also showed a couple students that had difficulty multiplying a two-digit by two-digit number how to do this task and the students were able to perform this task with a multiplication chart. The students either had myself or a classmate to check their study guide during class. Students can then go home try a blank copy of the study guide again and check their answers here.

Homework: The students were given three word problems and also told to study (they told me how to study in each class).

My Glass Half-Full Take: The basic premise of the school is that the student learns and the teacher teaches. It's that simple, but for me it has never been quite that simple. In the past, I would sometimes do the formative, make a generalization about all of my students and then reteach until I felt like the generalization changed. Today I picked certain students with precise standards in my mind that I had written down as students that still needed help with that standard based on assessment data. And I saw them get it. That's rewarding and gives me peace of mind with a quiz tomorrow.

One Thing to Do Differently: I asked students to journal two things for me. The first was to tell me two ways they intended to study. The second was to ask them to show me how to check their work on four select problems from the study guide (#7, 11, 14, and 17). I wish that I had an exemplar ahead of time for exactly what I meant. The number of questions I received - particularly for the second part of the journal activity was overwhelming. The students knew to use either the inverse operation or estimation for instance, but were writing that instead of showing the math and writing that. Perhaps I also could have been more clear in my prompt which was written using my Epson Projector.

And as a second thing to do differently, here are some formative assessments mistakes I collected from today (one of these I caught and helped the student out - the other I hope studies!).

Link of the Day: Percentage question from the site OpenMiddle: What is the fewest number of people surveyed if exactly 93.6% of people completed a survey?

Day Six: Using Estimation and Division

6th Grade Math Standards: MP1 Make sense of problems and persevere in solving them (see item #4 in the Agenda in Class #1)
MP3 Construct viable arguments and critique the reasoning of others.
6.NS.2 Fluently divide multi-digit numbers using the standard algorithm

The Learning Objective: Multiply factors to get a product; use division to find a quotient for one and two digit divisors; identify parts of a division problem

Quote of the Day: "Forbes Magazine reported in January of 2013 that only 8 percent of the resolutions we make are accomplished over one year's time. People burn out on their goals, or they never get started, or they get discouraged, and regardless of what happens they quit. If you hope to benefit from a one-day contract mentality, you need to make three promises: you will not quit, you will not procrastinate, and you will not allow discouragement to sideline you." - Rick Pitino

Agenda:

1. Estimation 180 (the first two stapler questions)
2. Review the multiplication homework
3. Notes and brief discussion about multiplication mistakes
4. Multiplication Word Problem: "If every class in the school had the exact same number of students as we have in math class right now, how many students would there be at Belmonte Middle School?"

End of Class 1

1. Division My Favorite No
2. Division Notes
3. Starting Division Homework
4. Division Ticket to Leave

End of Class 2 

*None of my three classes got exactly the same show. One of my classes did Estimation 180 as the last thing in class rather than the first thing for instance because they started the division topics in the class that they have with the other math teacher. Another class did not do the division ticket to leave because we went off on a tangent about what number multiplied by 5 is equivalent to 22 (more students had the answer shown below than the correct answer). 

The Assessment: In the second class, I tried to do a pre and post formative assessment to see what they knew about the dividend, divisor, and quotient. I threw a wrinkle in by giving variables instead of numbers and many students did the equivalent of run for the exits, but some caught on initially. In one class I did not get a post-assessment, but I will do it first thing tomorrow which is just as well.

The homework also served as an assessment as students were given about ten minutes in each class to get started and I went around to see how students were doing.

Homework: Students were given fifteen problems. Nine of these problems had double digit divisors. We talked about in our notes that students could either cover up the last digit of the divisor (I call it cover, cover), estimate, or use guess and check. I really believe estimation to be the most beneficial from a "what you'll do when your older and not in cell service" perspective, but I don't care as long as they have the fluency to get to the answer at this stage.

My Glass Half-Full Take: This was the second day we've used Estimation 180 and I continue to love the site for the energy it brings to a math classroom that students become accustomed to thinking there is only right and wrong. It is the perfect bridge to Math Practice 3 because students can disagree with one another in a tone that doesn't sound combative given that nobody is 100% certain there estimation is correct. Below is a picture of a student's work that was very sound, but ultimately incorrect. The student knew that there were 210 staples in each rod, so he used 210 as one factor. He looked at this picture and assumed that 12 was the other factor because the box appears to be stacked 3 rods by 4 rods. In reality the box actually fits 24 rods.

One Thing to Do Differently: I think my notes dragged on and I didn't give students enough time to digest the topic of two digit divisors. I feel as though my formative assessment on this topic left some students on an island as a result and will look to see who was left on that island when I check homework tomorrow.

Link of the Day: This is a New York Times article about a class called Big History. Among other things it touches upon are Bill Gates' motivations, grass roots versus government backed classes, the concept of interdisciplinary classes, and how education is tied to corporate America.

Day Five: Multiplying Factors to Find a Product

6th Grade Math Standards: 6.NS.3 Fluently add, subtract, multiply and divide multi-digit decimals using the standard algorithm.

MP3 Construct viable arguments and critique the reasoning of others

MP7 Look for and make use of structure.

The Learning Objective: Multiply factors to find a product.

Quote of the Day: "Give me 100 percent. You can't make up for a poor effort today by giving 110 percent tomorrow. You don't have 110 percent. You only have 100 percent and that's what I want from you right now." - John Wooden

Agenda:

I never did Estimation 180 Part II because I wanted to be sure we had plenty of time to work in the factor game. 

The Assessment: The first assessment took place during Estimation 180. As the students were doing this, I went around and checked their subtraction work from the third day of school. I was focusing specifically on checking their word problems to see if they wrote complete sentences. Why? I think the sentences give meaning to the problems in a way that can actually serve to help the students check their work. It's also important that students know how to write sentences and restate questions across the curriculum in ELA.

The next assessment took place as we were going over the jumpstart. I did days For each too low estimate I called on three students to see what they said was too low. I called on three different students for the too high problem and three more for the actual estimate. I asked why whenever I was getting an answer for the second time or if there was an answer that to me seemed radically different. I really enjoy Estimation 180 because it enables us to critique the reasoning of others in a stress free environment where anyone can be correct because nobody is certain of the answer for many of them. We did three different pictures from this site today each one building on the previous one (all three were about tissues). The last picture is where many students demonstrated MP7. In going around the room looking at different responses, the work for this problem caught my eye as an excellent reason for students to write too high and too low estimates prior to calculating.

Our third assessment came during the multiplication notes. I gave one problem for students to try on their own. After they were done, the students stood up and I went around to check. Eventually I outsourced my help and had students check in on another students. I really enjoy this technique as it gets students out of their seats and also enables them to contribute positively to the classroom culture of helping others.

A fourth assessment came in the form of a game called Pepper. I learned about this game a few years ago at a professional development activity from a very enthusiastic teacher. It is similar to the game Pepper that is played in baseball where fielders throw a ball to a person with a bat in close proximity to them and he/she gives a check swing back to the fielders peppering the ball to different people. What I do is have anywhere from five to seven students stand up and ask them vocabulary questions. If a student does not get the vocabulary correct, it is not a problem I simply call on a student until someone does and then call again on everyone who did not initially have it. The students enjoy the fast pace nature and I enjoy hearing correct definitions.

Assessment number five came as they got started on their homework and I went around the room to see how they were doing.

Homework: Multiplication practice

My Glass Half-Full Take: I always talk to the students about the value of getting sleep, but I need to get better at practicing what I preach. To this point in the year I have gotten 8 hours of sleep each night and it is allowing me to have more energy at the end of the day than I typically do. In all that is done to prepare a lesson and for that matter to prepare a teacher (graduate school, evaluations, professional development, etc.) I think sleep is as valuable as anything.

One Thing to Do Differently: I did much better explaining the Product Game (I kept calling it Factor Game during the day which didn't help either) to the second class I had than I did the first. I left out the details that they should use one board per partnership and that they should use the nine digits given at the bottom of the page for factors instead of numbers like 81 as factors. Next time I play this game or a game of any kind for that matter I will try to play it myself first rather than just go off the directions that I "feel confident" in.

Website of the Day: Wow. Addicting. Kids that play video games will be totally hooked. It's called 2048.

Day Four: The Baseline Takes Too Long

6th Grade Math Standards: Pretty much all of them.

The Learning Objective: The original objective was to multiply factors to find a product, but I did not anticipate the baseline would take up both classes.

Quote of the Day: "What do you know and what are you trying to find out?" - My graduate professor Kathy Favazaa

Agenda: This was my original plan minus the date which should say 9/8 but the student I have change it hadn't changed it yet:

The Assessment: The baseline consisted of thirty multiple choice questions. I have not seen the results of what we did, but students asked me several vocabulary questions particularly around the statistics unit.

Homework: I told students to have their supplies in class by tomorrow.

My Glass Half-Full Take: As students were finishing the jumpstart, I helped them on Pascal's Triangle and Visual Patterns. I even helped a couple students with subtraction. At times I was one on one, but I also went one on three or one on four in order to help them. They seemed eager to complete the problem. In my last class of the day I made them state "I will never give up on a problem" in unison. I believe that it is entirely up to an individual to change and that some of these individuals are going to make positive changes in the way they approach math this year.

One Thing to Do Differently: I never warned students about the baseline last week, and I meant to. Not that they would study or anything like that, but there are those students who like to come in and have a general idea what we'll be doing. I also feel like spending more than an hour on a baseline is somewhat wasteful. Looking at all the standards we need to hit though it would be hard to pick which questions we should eliminate.

Website of the Day: I thought this was a nice touch on why we write in math.

Day Three: Analyzing Subtraction Mistakes

6th Grade Math Standards: MP1 Make sense of problems and persevere in solving them.
MP3 Construct viable arguments and critique the reasoning of others.
MP6 Attend to precision.
MP8 Look for and express regularity in repeated reasoning.
3.NBT.2 (Yes! Third Grade Standards!) Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.

The Learning Objective: Subtract multi-digit numbers

Quote of the Day: I did not give a quote today. This as an idea is new for me this year. I have used it as a basketball coach and believe it can help set the tone for the mentality of the students day to day to over come adversity and stay humble through success. That being said, since it is new to me I have to start planning better and find a spot on my board for it. I'm thinking that it will go next to homework since that aspect of learning is almost entirely predicated on attitude.

Agenda:

Class #1:

• Jumpstart from Yummy Math on home field advantage in the NFL
• As students are worked on the jumpstart, I collected their homework which was the letters in the person of their fifth grade teachers and their signed syllabus. The percentage of homework that was turned in was over 90%. 
• My Favorite No. If you haven't seen the magic of My Favorite No as an assessment watch this video 
• Operations vocabulary notes: Sum and difference

Class #2:

• Homework formatting. All of the teachers in the sixth grade frequently have students use their notebooks to do homework assignments that involve worksheets. The reasons are obvious - the students will need more space to do work and can keep a kind of running diary of what they have learned. We also discussed numbering each problem. It perplexes me that this is even an issue, but it is. 
• Approaching word problems. Myself and the other three math teachers have agreed that there are three essentials that students should get used to in regards to word problems: the students must circle what they know, underline what they're trying to find out, and restate the prompt (students call it turning the question around). 
• Students could then start the rest of the homework (18 problems) and in many cases finish the homework assignment. 
• I gave students the first 4 rows of Pascal's Triangle and had them try to find the numbers in the next 4 rows (Math Practice 8).
• One student was able to complete this so I gave her a copy of the first two Visual Patterns as another challenge 
• The students did a ticket to leave that asked them to solve 5092 - 1375

The Assessment: The My Favorite No question was shown below

Homework: Whole Numbers Review A, students should have supplies bought and in class by Tuesday, and the students that did not turn in their syllabus signed need that by Tuesday.

My Glass Half-Full Take: Last June when a colleague and I learned that we would need revamp our curriculum map since we were changing the structure of our math classes we initially thought we would leave out the whole number review unit. This unit is nowhere to be found in the sixth grade standards, and if an education consultant were to see our map the first thing that would be scrutinized would probably be the fact that we teach standards that in some cases go as low as the third grade. I am well aware that much of the blame for the U.S. dragging behind Finland, Singapore, and other nations in mathematics education today is a result of lowering the bar for our students, but before this hypothetical consultant jumps down my throat let me explain why today will be a valuable day for me as an educator this year and more importantly my students.

First of all, it was the third day of school. For intimidated sixth graders in a new building. Using a locker for the first time. With a lock. That won't open. An entirely different schedule. That includes eight different teachers compared to one. In seven different rooms (no - not eight rooms).  And mingling with new peers. From four different elementary schools. Not to mention the five new students from five different districts. There's a time and place for high standards, but even folks joining the army fill out forms before being sent to boot camp.

Second of all, these students were assessed and the results indicated that not everyone had mastered this standard. In fact, in one of my three classes, nine out of twenty students did not give the correct answer of 1,088. Call it rust, call it nerves, or whatever you like - I'm pretty sure that if 45% of students were not ready to demonstrate a third grade standard out of the chute, they may have had even higher anxiety about the new school year than they already did if we started with sixth grade standards. Subtraction is an issue of math fluency. If the gaps students have with borrowing or checking their work are not at least addressed before tackling the sixth grade curriculum, it would be the equivalent of asking a scuba diver to navigate The Great Barrier Reef without an oxygen tank.

 

Third, I did challenge the students after they had gone through the homework. The majority of students had more than 10 minutes to derive rows five through eight of Pascal's Triangle, and only one student could do it. I had to continuously point at my poster of Albert Einstein and his quote, "It's not that I'm so smart - it's that I stay with problems longer." These students were able to get some but not all of the numbers in Pascal's Triangle. They shared with me different ideas of what the pattern could and could not be. They argued with the person next to them about why every number in the fifth row would be one and four. Most students ended up exhausting half of the list of Mathematics Practice Standards. So for the majority of students who have mastered the third grade standard, this class was still a learning experience.

Fourth, with the two classes I saw twice, I did a post-assessment. All I did was change the numbers from the pre-assessment. These two classes went from 62% answering the problem correctly to 79% answering correctly. And for the 21% that still do not have mastery, I will continue to work with them on this issue because everyone should swim with the fishes in the Great Barrier Reef.

Fifth, look at the wrong answers. Who's to say this habit is easy to break? This is the perfect time to explain to students the value of checking the work (see the right answer). Even confident students can agree to making simple mistakes and this leads to a nice conversation about analyzing what can go wrong in any given problem and how to filter out these mistakes.

I am glad that we are going to give the students review for an opening unit. When the bell rang at the end of the day I felt as though most students had come away better thinkers than they were entering the day. This unit serves as the foundation for how the students will see different tasks based on their own personal potential and will be asked to analyze these tasks on different levels of Bloom's Taxonomy.

Where I'd Throw the Red (Challenge) Flag: I did not give a post-assessment to the class that I share with another teacher. It was unfortunate because this can be an excellent indicator not only of who still needs help on subtraction, but also about what learning styles work and do not work for certain students. The problem was that I did not think about doing this ticket to leave until the middle of the day, and obviously never had the opportunity to relay the message. This is not atypical for me and I imagine most teachers to come up with and implement a new idea on the fly.

Valuable Website Visit of the Day: Estimation 180 - Monday will mark the first of several visits to the land of making sense of guessing.